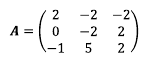CS STUDY

행렬을 가우스 행렬의 형태로 바꿀 때 곱하는 수를 기억해야 한다. 이때, 행렬 A의 주 대각 원소를 1로 바꾸기 위해 곱하는 수의 역수는 행렬 L의 주 대각 원소가 된다. 그리고 행렬 A의 주 대각 원소 아래에 위치한 원소를 0으로 만들기 위해 필요한 배수의 음수를 행렬 L의 위치에 놓는다. 1. 먼저 1행 1열의 원소를 1로 만들기 위해 1행에 1/2를 곱한다. 이를 계산하면 다음과 같다. 이는 주대각 원소를 1로 바꾸기 위한 연산이였으므로 앞서 곱한 수 1/2의 역수인 2가 행렬의 1행 1열 원소가 된다. 2. 3행 1열 원소를 0으로 만들기 위해 3행에 1행을 더한다. 이때, 1행에 따로 곱하는 수는 없으므로 배수는 1에 해당한다. 3행 1열의 원소는 주 대각 원소가 아닌 주 대각 원소 아래에 위치..

1. LU분해의 개념 가우시안 소거밥이나 가우스-조르단 소거법은 행렬의 크기가 작을 때는 괜찮지만, 행렬의 크기가 커지면 메모리 문제, 반올림 문제, 속도 문제 등 여러 문제가 발생할 수 있다. 이러한 문제를 LU분해를 통해 해결할 수 있다. 우리가 풀고자 하는 선형 방정식운 n개의 방정식으로 구성된 Ax=b 형태이다. 정사각 행렬 A를 다음과 같이 행렬 L과 U의 곱으로 분해하겠다. 위 식처럼 분해하는 방법을 LU분해(LU factorization)라고 한다. 2. LU분해 방법 LU 분해의 목표는 행렬 A를 하 삼각 행렬 L과 상 삼각 행렬 U로 분해하는 것이다. LU분해에서 상 삼각 행렬 U는 가우스 행렬이고 이는 행렬 A를 가우스 행렬 U로 변환하는 과정에서 행렬 L을 구할 수 있다는 것을 의미한..

1. 기본 행렬의 개념 LU분해 과정을 이해하기 위해 기본행렬은 알아야 하는 행렬이다. 기본 행렬(elementary matrix)는 단위 행렬에서 기본 행 연산을 수행한 행렬이다. 위 그림은 3x3 크기의 단위 행렬에서 1행에 3을 곱해서 2행에 더하는 기본 행 연산을 수행하면 기본 행렬 E로 변하게 된다. 2. 기본 행렬의 역행렬 기본 행렬의 역행렬은 일반적인 행렬의 역행렬에 비해 쉽게 구할 수 있다. 먼저 기본 행렬이 대각 행렬인 경우 행렬 원소의 주 대각 원소만 0이 아닌 대각 행렬의 역행렬은 주 대각 원소의 역수를 대입하면 구할 수 있다. 기본 행렬이 대각 행렬이 아닌 경우에는 주대각 원소 이외에도 0이 아닌 원소가 존재한다는 의미이므로 대각 행렬의 역행렬을 구하는 방법은 사용할 수 없다. 위와..

1. 대각화의 개념 행렬의 대각화(diagonalization)는 이름 그대로 행렬을 대각 행렬로 만드는 것을 의미한다. 정사각 행렬 A에 대해 P-1AP가 대각 행렬이 되는 가역 행렬 P가 존재하면 행렬 A는 대각화가능이라고 한다. 행렬의 대각화 가능 여부는 해당 행렬의 고윳값의 개수를 보면 판단할 수 있다. nxn 크기의 행렬 A가 대각화 가능하려면 행렬 A는 n개의 서로다른 고윳값을 가져야 한다. 2. 직교 대각화의 개념 먼저 직교 닮음에 대해 복습해보면 다음 식이였는데 위 식에서 정사각 행렬 B가 대각 행렬 D라면 다음 식을 만족하는 직교 행렬 P가 존재하는 경우이다. 위와 같은 경우, 직교 행렬 P는 A를 '직교 대각화' 한다고 말하며, A는 '직교 대각화 가능'하다고 말한다. 이는 행렬 A에 ..

1. 닮음의 개념 행렬 간에도 닮음이라는 표현을 사용하는데 다음 식을 만족하는 가역행렬 P가 존재할 때, 정사각 행렬 A,B는 서로 닮음이라고 한다. 이때 행렬 A,B는 정사각 행렬이어야 하므로 행 크기와 열 크기가 같다. 그리고 행렬 P는 '가역 행렬'이므로 역행렬이 존재한다. 또한 위 식을 만족하는 직교 행렬 P가 존재할 때 행렬 B는 행렬 A에 직교 닮음이라고 한다. 2. 닮음의 성질 (1) 서로 닮은 행렬의 행렬식은 동일하다. (2) 행렬 A가 가역 행렬이라는 말은 P-1AP가 가역 행렬이라는 말과 같다. (3) 행렬 A와 행렬 P-1AP의 랭크와 널리티는 동일하다. (4) 행렬 A와 행렬 P-1AP의 대각합은 동일하다. (5) 행렬 A와 행렬 P-1AP의 고윳값은 동일하다. 넘파이로 직교 대각 ..

직교 행렬(orthogonal matrix)이란 어떤 행렬의 행 벡터와 열 벡터가 유클리드 공간의 정규 직교를 이루는 행렬을 의미한다. 그리고 '직교'라는 단어는 벡터 사이 각도가 90도임을 의미한다. 사이 각도가 90도라는 말은 두 벡터의 내적값이 0이라는 뜻이다. 정규직교행렬은 행렬을 구성하는 각 행 벡터 혹은 열 벡터의 길이가 1이며 서로 수직인 벡터로 이루어진 행렬을 의미한다. 직교 행렬은 자기 자신과 자신의 전치 행렬을 행렬 곱하면 단위 행렬이 된다. 위 식은 직교 행렬 A의 역행렬은 자기 자신의 전치 행렬임을 의미한다.

1. 2x2 행렬의 고윳값과 고유 벡터 구하기 위 식은 동차 선형 시스템이라고 볼 수 있다. 위 식에서 고윳값 람다가 존재하기 위한 필요충분조건은 괄호 안의 행렬식이 0이 되는 것이다. 위와 같은 식을 특성 방정식이라고 한다. 다음은 이렇게 구한 고윳값을 이용해 고유 벡터를 구해 보겠다. 두 가지 경우를 나누어서 구한다. 이런 식으로 구하면 람다가 -1일때도 구할수 있다. 2. 3x3 행렬의 고윳값과 고유 벡터 구하기 람다가 3인 경우만 고유 벡터를 구해 보자. 따라서, 앞서 구한 A-3I를 이용하면 동차 선형 시스템은 다음과 같이 나타낼 수 있다. 위 동차 선형 시스템을 풀기 위해 가우스 행렬로 정리해 보겠다. 고유 벡터의 길이가 1이 되게끔 정규화 하면 고유 벡터는 다음과 같다. 3. 성질 (1) (..

고윳값은 영어로 eigenvalue라고 하는데 이때, 쓰이는 단어인 eigen은 특성이라는 뜻을 담고 있다. 즉, 고윳값, 고유 벡터는 특성값, 특성 벡터라고 생각할 수 있고, 이들은 행렬의 특성을 나타낸다. 벡터는 방향과 크기로 구성되는데, 고윳값, 고유 벡터에서 말하는 특성이란 벡터의 방향은 변하지 않고 크기만 변하는 특성을 의미한다. 즉, 고유 벡터(eigenvector)란 벡터에 선형 변환했을 때, 방향은 변하지 않고 크기만 변하는 벡터를 의미한다. 또한 선형 변환 이후 변환 크기를 고윳값이라고 한다. 고윳값과 고유 벡터를 수식으로 나타내면 다음과 같다. 위 수식에서 좌변은 벡터 x에 선형 변환 A를 취한 것을 의미한다. 이는 우변과 동일한데 우변은 기존 벡터 x의 방향은 변하지 않고 길이가 람다..

1. 벡터곱의 정의 벡터 곱 또는 크로스 곱은 3차원 공간의 벡터들 간에 적용할 수 있는 연산이다. 단위 벡터 i,j,k를 사용해 벡터 u와 벡터 v의 벡터 곱 uxv를 다음과 같이 표현할 수 있다. 벡터 곱 uxv는 벡터 u와 벡터 v에 수직인 벡터를 의미한다. 2. 벡터 곱의 기하학적 의미 위 그림은 벡터 u와 벡터 v의 벡터 곱 uxv는 벡터 u와도 수직이고 벡터 v와도 수직인 벡터이다. 위 그림은 벡터 u와 벡터 v가 평행할 경우에는 벡터 곱의 크기가 0임을 알 수 있다. 위 그림은 벡터 곱의 기하학적 의미를 나타낸다. 벡터 u와 벡터 v가 만드는 평행사변형의 넓이는 벡터 u와 벡터 v의 벡터 곱의 노름(norm)과 같다. 이를 수식으로 나타내면 다음과 같다. 3. 스칼라 삼중 곱 벡터 u,v,w..

1. 벡터의 외적 외적(outer product) 또는 텐서 곱(tensor product)은 다음과 같은 연산을 의미한다. 벡터 u와 v가 존재할 때, 두 벡터의 외적을 구하면 다음과 같다. 2, 크로네커 곱 크로네커 곱은 외적의 특별한 경우이다. 행렬 A가 nxp 행렬이고 행렬 B가 mxd 행렬일때 행렬 A와 행렬 B의 크로네커 곱 AxB는 크기가 nmxpd인 행렬이다.