1. 대각화의 개념
행렬의 대각화(diagonalization)는 이름 그대로 행렬을 대각 행렬로 만드는 것을 의미한다.
정사각 행렬 A에 대해 P-1AP가 대각 행렬이 되는 가역 행렬 P가 존재하면 행렬 A는 대각화가능이라고 한다.
행렬의 대각화 가능 여부는 해당 행렬의 고윳값의 개수를 보면 판단할 수 있다. nxn 크기의 행렬 A가 대각화 가능하려면 행렬 A는 n개의 서로다른 고윳값을 가져야 한다.
2. 직교 대각화의 개념
먼저 직교 닮음에 대해 복습해보면 다음 식이였는데

위 식에서 정사각 행렬 B가 대각 행렬 D라면 다음 식을 만족하는 직교 행렬 P가 존재하는 경우이다.

위와 같은 경우, 직교 행렬 P는 A를 '직교 대각화' 한다고 말하며, A는 '직교 대각화 가능'하다고 말한다. 이는 행렬 A에 선형 변환을 취한 결과, 대각 원소만 남는 대각 행렬이 된다고 생각하면 된다.
크기 nxn 행렬 A가 직교 대각화 하려면 다음 조건을 만족해야 한다.

대칭 행렬은 At=A 을 만족하는 행렬이다.

3. 고윳값 분해
고윳값 분해(eigenvalue decomposition)는 직교 대각화의 한 종류이다. 직교 벡터 P는 고윳값 분해에서는 고유 벡터를 이용해 만들 수 있고, 대각 행렬의 원소에 해당하는 것이 고윳값이라고 생각하면 된다.
대칭행렬 A의 고윳값과 고유 벡터가 존재할 때 A의 고윳값 분해는 아래와 같다. 고윳값 분해는 행렬을 고유 벡터, 고윳값의 곱으로 분해하는 것을 의미한다.


4. 특이값 분해
특이값 분해(Singular Value Decomposition)는 행렬을 분해하는 방법 중 하나로 정사각 행렬을 대상으로 하는 고윳값 분해를 mxn 행렬로 일반화시킨 것을 의미한다.
특이값 분해는 행렬의 차원 축소를 위한 도구로 사용된다. 실제로 머신러닝 분야 중 주성분 분석과 같은 차원 축소 분야에서 특이값 분해가 많이 쓰인다.
다음 그림은 3차원 데이터를 2차원으로 줄이는 것을 나타낸다.
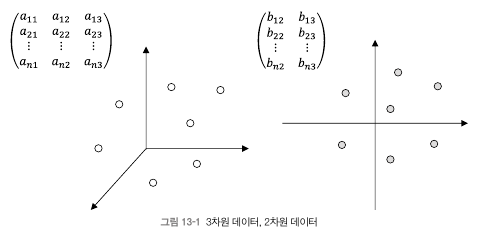
만약 행렬 A가 p차원이라고 했을 때, 행렬 A를 d차원(p>d)로 축소한 행렬을 B라고 하면, 결국 특이값 분해는 차원 축소 행렬 B를 찾는 데에 사용된다.

위 그림을 보았을 때, 행렬 A의 크기가 nxp라는 말은 p차원에 n개의 점이 존재한다고 생각할 수 있다. 그리고 행렬 A를 차원 축소시키는 것의 의미는 행렬 A의 n개의 점을 표현 할 수 있는 기존 p보다 작은 차원인 d차원의 부분 공간을 찾는 문제라고 볼 수 있다.






넘파이로 고윳값 분해 실습
import numpy as np
A=np.array([[1,2,3],[2,4,5],[3,5,3]])
E,V=np.linalg.eig(A)
print(E) #[ 9.90754321 0.05152112 -1.95906434]
print(V)
'''
[[-0.36762518 -0.82102902 -0.43676432]
[-0.67017224 0.55950483 -0.48767152]
[-0.64476422 -0.11342699 0.75591892]]
'''
넘파이로 특이값 분해 실습
import numpy as np
B=[[3,6],[2,3],[1,2],[5,5]]
U,S,Vt=np.linalg.svd(B)
print(U)
'''
[[-0.6305882 0.65070051 -0.34404196 0.24613512]
[-0.34294608 0.0720764 0.09856768 -0.93138466]
[-0.21019607 0.21690017 0.9335582 0.19297931]
[-0.66375005 -0.72411888 -0.01971354 0.18627693]]
'''
print(S) # 특이값들만 반환
'''
[10.50804076 1.6065738 ]
'''
print(Vt)
'''
[-0.58113622 -0.8138063 ]
[-0.8138063 0.58113622]]
''''Mathematics > Linear algebra' 카테고리의 다른 글
| LU분해 (0) | 2022.03.03 |
|---|---|
| 기본 행렬 (0) | 2022.03.03 |
| 닮음 (0) | 2022.03.01 |
| 직교 행렬의 개념 (0) | 2022.03.01 |
| 고윳값과 고유 벡터 계산, 성질 (0) | 2022.02.28 |