정규분포는 가우스 분포라고도 한다. 표본개수가 많아지면 표본평균은 원래 확률변수가 정규분포가 아니어도 근사적으로 정규분포를 따른다는 중심극한정리의 의하여 더욱더 정규분포에 대한 이해가 필요하게 되었다. 정규분포는 확률변수가 연속인 경우에 적용이 되며 확률 밀도함수는 다음과 같다.


정규분포의 모습과 성질에 대하여 알아보도록 하자. 확률변수 X가 정규분포를 따른다라는 것을 다음과 같은 기호를 사용한다.
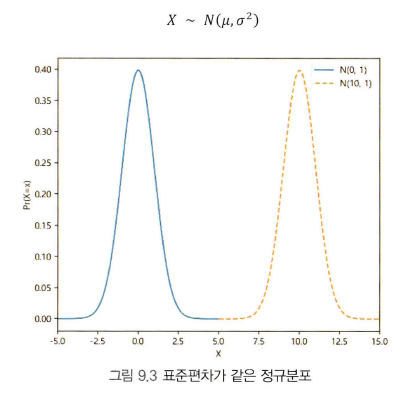
위 그림은 평균이 다르고 분산이 같은 2개의 정규분포 그림이다. 그림과 같이 평균의 변화는 평균만큼 분포를 평행이동한 것과 같다.
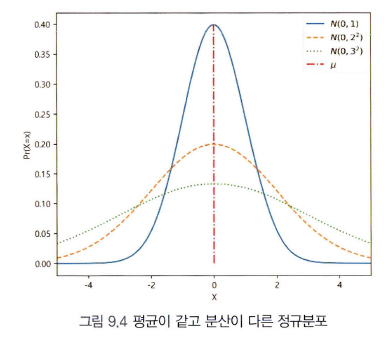
위 그림은 평균이 같지만 분산이 다른 경우이다. 똑같은 평균값을 주지만 분산, 즉 표준편차가 큰 경우에는 데이터의 산포가 넓게 흩어져 있음을 알 수 있다.
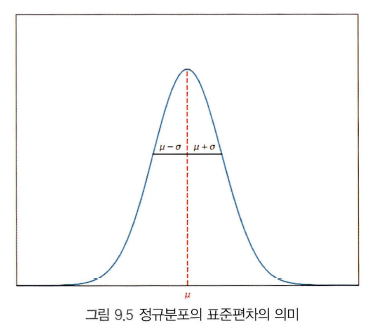
위 그림은 정규분포의 표준편차는 평균에서의 일정한 거리를 나타낸다. 정규분포에서의 표준편차는 볼록함수에서 오목함수로 바뀌는 변곡점을 의미한다.



# 확률값 구하기
np.round(ss.norm.cdf(1) - ss.norm.cdf(-1),3)
# 0.683
np.round(ss.norm.cdf(2) - ss.norm.cdf(-2),3)
# 0.954
np.round(ss.norm.cdf(3) - ss.norm.cdf(-3),3)
# 0.997
'Mathematics > probability statistics' 카테고리의 다른 글
| 표본평균의 분포 (0) | 2022.03.27 |
|---|---|
| 임의표본 (0) | 2022.03.27 |
| 이항분포 (0) | 2022.03.26 |
| 베르누이 분포 (0) | 2022.03.26 |
| 독립 (0) | 2022.03.26 |