

A=[2,3]
trials=5
scipy.special.comb(trials,A)
# array([10., 10.])

ex) 성공확률이 1/3이고 시행횟수가 5인 이항분포의 확률밀도함수의 합이 1임을 확인해보자.
trials=5
A=np.arange(0,6)
event_prob=1/3
ss.binom.pmf(A,n=trials,p=event_prob).sum().round(3)
# 1.0
적률생성함수는 다음과 같이 계산된다.
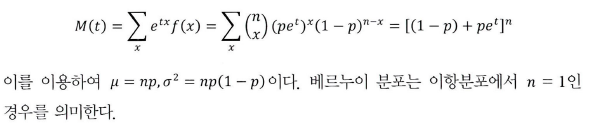

# 적률생성함수를 이용한 평균과 분산을 구해보자
p,t,n = sympy.symbols('p,t,n')
expr=((1-p) + p * sympy.exp(t)) ** n
# 1차 적률(기댓값)
EX=expr.diff(t,1).subs({'t':0})
EX # np# 2차 적률
EXX=expr.diff(t,2).subs({'t':0})
EXX
# 분산
(EXX - EX**2).together()
'Mathematics > probability statistics' 카테고리의 다른 글
| 임의표본 (0) | 2022.03.27 |
|---|---|
| 정규분포 (0) | 2022.03.26 |
| 베르누이 분포 (0) | 2022.03.26 |
| 독립 (0) | 2022.03.26 |
| 상관계수 (0) | 2022.03.26 |