HFWS 데이터는 통계청 마이크로 데이터 서비스에서 제공하는 2018년 세대별 가계금융복지 조사 결과이다.
#
# 데이터 구성
#
# [HFWS] 데이터: “가계금융복지조사( 2017년 이후) > 가구마스터(제공)[2018가구금융복지조사]”
df = pd.read_csv('https://github.com/bong-ju-kang/kmu-mba-statistics/raw/master/Data/MDIS_2018_HFWS.txt',
header=None)
df.head(2)
# 가구당 연간 소득액: 100번쨰
income=df[109]
np.round(np.mean(income),1)
연간소득에 대한 평균값과 표준편차를 구해보자.
# 모집단으로 가정
# 모편균, 모표준편차
np.round([np.mean(income),np.std(income,ddof=0)],1)
확률변수 X를 가계소득이라고 하면 (u,o)=(5364.0, 5818.4)인 어떤 분포를 따른다고 할 수 있다. 이때 이 분포에서 크기가 100인 임의표본(random sample) X1,...,X100을 추출하여 그 평균을 구해보자.
# 크기가 100인 임의 표본 1개의 표본 평균
size=100
np.random.seed(1)
# 비복원 추출
index=np.random.choice(len(income),size,replace=False)
sample_mean=np.mean(income[index])
np.round(sample_mean,1)
# 표본 비율
np.round(size/len(income),4)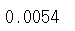
원래 모평균값은 5364이지만 임의표본 1개에 대한 평균값은 5323.1이 된다. 큰 차이는 아니지만 통계적으로 0.54%의 표본을 갖고서 나름대로 의미 있는 추정이 된다. 그런데 얼마나 의미 있는지는 평균의 분포를 알아야만 판단할 수 있다.
그럼 위 데이터에서 100개의 임의표본을 1000번 반복적으로 추출한다고 가정했을 때 그 평균의 분포를 살펴보자.
# 표본평균의 평균
num_samples=1000
size=100
result=[]
np.random.seed(123)
for i in np.arange(num_samples):
index=np.random.choice(len(income),size,replace=False)
result.append(np.mean(income[index]))
np.round(np.mean(result),2)
결과를 보면 모평균값과 표본평균의 평균값이 거의 일치함을 알 수 있다. 표본평균으로 모평균을 추정하고자 하는 경우에 표본평균은 하나의 통계량이 되며 이 분포를 표본분포(sampling distribution)라고 정의할 수 있다. 즉 통계량은 미지의 모수(parameter)에 의존하지 않는 하나 이상의 확률변수의 함수이다.
그러나 통계량을 만드는 목적이 모집단의 특성이라고 할 수 있는 모수를 추정하기 위한 것이므로 그 분포는 모수에 의존하게 된다.
표본분포를 알아야 하는 이유는 추정의 확률적 정확도를 제시할 수 있기 때문이다. 즉, 위의 예에서 다음과 같은 확률을 정의할 수 있다.

여기서, 표본평균으로 모평균을 예측할 때 그 차가 100, 즉 가계소득 단위가 만 원이므로 백만 원 이하일 확률을 구할 수 있는 것이다.

'Mathematics > probability statistics' 카테고리의 다른 글
| 카이제곱분포 (0) | 2022.03.27 |
|---|---|
| 표본평균의 분포 (0) | 2022.03.27 |
| 정규분포 (0) | 2022.03.26 |
| 이항분포 (0) | 2022.03.26 |
| 베르누이 분포 (0) | 2022.03.26 |