특정 통계량의 표본분포를 구할 때 핵심이 되는 몇 가지 분포 중에 카이제곱분포에 대하여 알아보겠다.

이때 표본분산은 모분산의 추론에 중요한 역할을 하는데 이의 분포를 정의할 때 카이제곱분포를 사용한다.


위 그림을 보면 자유도가 클수록 카이제곱 확률밀도함수는 점점 평평해짐을 알 수 있고, 당연히 제곱합이므로 0보다 큰 구간에서만 정의되어 있다. 적률생성함수는 다음과 같이 계산된다.


# 적률생성함수를 이용한 평균과 분산 계산
k,t=sympy.symbols('k,t')
expr=(1-2*t) ** (-k/2)
# 1차 적률(기댓값)
M1=sympy.Lambda(t,expr.diff(t).simplify())
EX=M1(0)
EX #k# 2차 적률
M2=sympy.Lambda(t,expr.diff(t,t).simplify())
EXX=M2(0)
EXX
# 분산
(EXX-EX**2).simplify()
카이제곱분포의 중요한 성질 중의 하나는 가법성(additivity)이다.




- 분산이 같은 두 정규모집단에서 표본분산의 분포

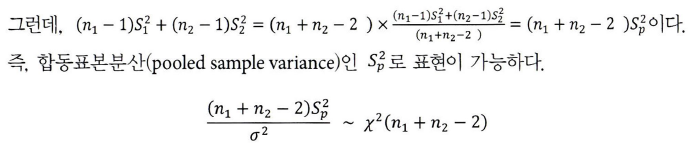

'Mathematics > probability statistics' 카테고리의 다른 글
| F분포 (0) | 2022.03.27 |
|---|---|
| (스튜던트)t분포 (0) | 2022.03.27 |
| 표본평균의 분포 (0) | 2022.03.27 |
| 임의표본 (0) | 2022.03.27 |
| 정규분포 (0) | 2022.03.26 |