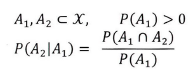CS STUDY

2개의 확률변수 X1,X2에 대한 결합확률밀도함수를 f(x1,x2)라고 하면, 조건부확률밀도함수를 이용하여 결합확률밀도함수는 다음과 같이 정의할 수 있다. 즉 X1=x1이 주어진 경우에 X2의 주변확률밀도함수가 어떠한 x1 값에도 불구하고 의존하지 않는 것을 의미한다. 일반적으로 2개의 확률변수가 확률적으로 독립이기 위한 필요충분조건은 2개의 확률변수가 독립인 경우의 중요 # 두 변수 간의 독립성 여부 확인 fxy.check_independence(['X'],['Y'])

이를 프로그램으로 확인해보자. # 결합확률 정의 prob=np.array([2,4,3,1,1,4])/15 fxy=JPD(['X','Y'],[2,3],prob) print(fxy) # 확률분포 확인 np.sum(fxy.values) # 1.0 # X주변확률 구하기 fx=fxy.marginal_distribution(['X'],inplace=False) print(fx) # X의 기댓값 구하기 x=np.array([1,2]) EX=np.dot(x,fx.values) EX.round(3) # 1.4 # X의 제곱 기댓값 구하기 EXX=np.dot(x*x,fx.values) EXX.round(3) # 2.2 # x의 표준편차 구하기 SDX=np.sqrt(EXX-EX**2) SDX.round(3) # 0.49 #..

import numpy as np import scipy from scipy import linalg as la import matplotlib.pyplot as plt import scipy.stats as ss import sympy from pgmpy.factors.discrete import JointProbabilityDistribution as JPD import pgmpy # 결합 확률 정의 prob=list() for i in np.arange(1,4): for j in np.arange(1,3): prob.append((i+j)/21) fxy=JPD(['X1','X2'],[3,2],prob) print(fxy) np.sum(fxy.values) # 1.0 # 주변 확률 구하기 fx=fxy..

새로운 사건 w2⊂Ω를 고려했을 때 상대적으로 w1을 표본공간으로 하는 확률은 사건 w1이 주어져 있을때 사건 w2의 조건부확률(conditional probability)라고 한다. 예를 들어, 주머니 속에 빨간 돌이 3개, 파란 돌이 5개 있을 때, 임의로 빼낸 돌은 다시 넣지 않고(비복원) 연속적으로 돌을 꺼낸다고 하자. 이때 첫 번째 꺼낸 돌이 빨간 돌(w1)일 때 두 번째 꺼낸 돌(w2)이 파란 돌일 확률을 구하는 것이다. 이 예에서 관심이 있는 표본 공간은 첫 번째 꺼낸 돌이 빨간 돌인 공간이다. 이런 의미에서 두 번째 꺼낸 돌이 파란 돌일 사건 중에서 관심이 있는 사건은 w1∩w2이다. 따라서 조건부확률을 다음과 같이 정의할 수 있다. 이를 확률 변수 관점으로 정의하게 되면 다음과 같다.

X가 확률변수일 때의 기댓값(expectation)을 다음과 같이 정의한다. 연속확률변수인 경우에는 적분으로 변경하면 된다. 기댓값은 X가 가질 수 있는 값이 x1,x2,,,xn일 때 이 값들의 가중평균(weight average)이라고 할 수 있다. 이런 의미에서 E(X)를 X의 평균값이라고 한다. 수학적 기댓값 중에서 또다른 중요한 기댓값은 분산이다. u=E(X)라고 하자. 이 값은 평균과의 차이에 제곱, 즉 평균과의 편차 제곱에 대한 가중평균이라고 할 수 있다. 이 값을 확률변수 X의 분산이라고 하며 일반적으로 아래 기호를 사용한다. 분산의 양의 제곱근을 표준편차 라고 한다. import sympy x=sympy.Symbol('x') mu=sympy.integrate(x*1/2, (x, -1,1))..

확률변수는 표본공간(M)이 주어져 있을 때, 함수 X가 모든 c=M에 대하여 딱 한 개의 숫자만을 할당하는 경우, 즉 X(c)=x, 이 함수를 확률변수라고 한다. 여기서 X 공간을 X={x:x = X(c), c(=M)라고 정의하자. 따라서 확률변수는 표본공간에서 정의된 함수이며 결과는 항상 실수값이다. 1. 이산형 확률밀도함수 ex) import scipy.special import numpy as np A=[0,1,2] trials=4 event_prob=1/2 np.sum(scipy.special.comb(trials,A) * event_prob ** trials) 2. 연속형 확률밀도함수 연속형 확률밀도함수는 다음과 같이 정의한다. ex) # 특정 이벤트의 확률 구하기 x=sympy.Symbol('..

확률이론에서 하나의 실험이나 시행은 가능한 모든 결과가 정의되어 있고 무한히 반복 가능한 절차를 의미한다. 무작위 시행은 가능한 결과가 2개 이상인 시행이다. 무작위 시행을 확률 시행이라고 명명하자. 여기서 가능한 모든 결과의 집합을 표본 공간(sample space). 이때 하나의 시행의 결과가 wㅈ에 속하면 사건 w가 일어났다고 한다. 만약 이러한 시행을 N번 반복했고 그중 f번만큼 w가 일어났다고 한다면 f/N을 계산할 수 있다. 이 값을 상대도수(releative frequency)라고 한다. 시행한 횟수가 많을 경우에는 상대도수 값이 특정 값으로 안정화되는 경향이 있다. 그 값을 p라고 한다면 미래의 시행에서 해당 사건은 그 값만큼 일어날 것이라고 생각할 수 있다. 이 값을 사건 w에 대한 확률..