확률변수는 표본공간(M)이 주어져 있을 때, 함수 X가 모든 c=M에 대하여 딱 한 개의 숫자만을 할당하는 경우, 즉 X(c)=x, 이 함수를 확률변수라고 한다. 여기서 X 공간을 X={x:x = X(c), c(=M)라고 정의하자. 따라서 확률변수는 표본공간에서 정의된 함수이며 결과는 항상 실수값이다.



1. 이산형 확률밀도함수

ex)

import scipy.special
import numpy as np
A=[0,1,2]
trials=4
event_prob=1/2
np.sum(scipy.special.comb(trials,A) * event_prob ** trials)2. 연속형 확률밀도함수
연속형 확률밀도함수는 다음과 같이 정의한다.

ex)

# 특정 이벤트의 확률 구하기
x=sympy.Symbol('x')
PA=sympy.integrate(sympy.exp(-x),(x,0,1))
PA
3. 분포함수

분포함수의 몇 가지 성질



a,b,x=sympy.symbols('a,b,x')
F=sympy.Lambda((x,a,b),(x-a)/(b-a))
F(x,0,1)
import scipy.stats as ss
x=np.linspace(0,1,100)
cdf_x=x
fig,ax=plt.subplots(figsize=(7,7))
ax.plot(x,cdf_x)
ax.set_xlabel("균등확률변수값")
ax.set_ylabel("F(x)=Pr(X<=x)")
plt.tight_layout()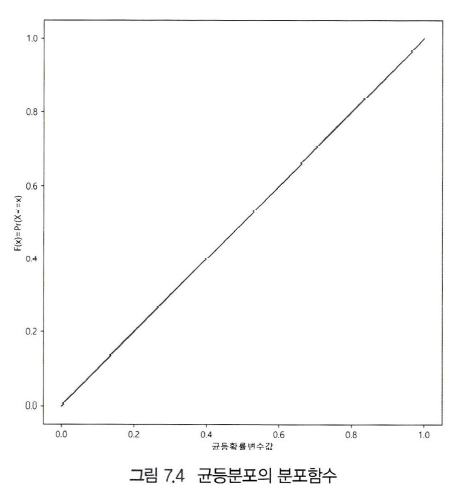
'Mathematics > probability statistics' 카테고리의 다른 글
| 상관계수 (0) | 2022.03.26 |
|---|---|
| 주변분포와 조건부분포 (0) | 2022.03.26 |
| 조건부확률 (0) | 2022.03.26 |
| 기댓값 (0) | 2022.03.23 |
| 확률 시행과 표본 공간, 사건과 상대도수 (0) | 2022.03.22 |