1. 역행렬의 개념
행렬 A의 역행렬이란 AB=I를 만족하는 행렬 B를 의미한다.
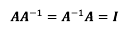
역행렬은 구하고자 하는 행렬의 행렬식이 0일때, 역행렬은 존재하지 않는다.
어떤 행렬의 역행렬이 존재하는 경우 해당 행렬을 가역 행렬(invertible matrix)이라고 부르며 가역 행렬의 역행렬은 유일하다.
행렬 A의 역행렬이 존재하지 않으면 행렬 A를 특이 행렬(singular matrix)라고 한다.
2. 역행렬 계산
1) 2x2 행렬의 역행렬 구하기
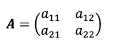

행렬 A,B가 크기가 같고, 두 행렬 모두 가역 행렬이면 두 행렬의 행렬 곱 AB또한 가역이며 다음과 같은 성질을 따른다.
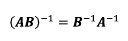
2) nxn 행렬의 역행렬 구하기
여인수를 이용하면 행렬 A의 역행렬을 구할 때 사용하는 여인수 행렬을 구할 수 있는데 행렬 A의 여인수로 구성된 다음과 같은 행렬을 여인수 행렬(maxtrix of cofactors from A)라고 한다.
여인수 행렬의 전치 행렬을 행렬 A의 수반 행렬(adjoint of A)라고 하며 adj(A)로 나타낸다.
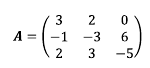
행렬 A의 여인수 행렬을 구하기 위해 여인수를 구해보자.
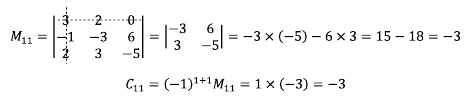

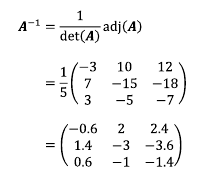
3. 정사각 행렬의 거듭 제곱

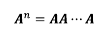
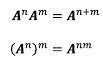
'Mathematics > Linear algebra' 카테고리의 다른 글
| 벡터 공간 (0) | 2022.02.25 |
|---|---|
| 역행렬의 성질 (0) | 2022.02.25 |
| 행렬식의 성질 (0) | 2022.02.25 |
| 행렬식의 계산 (0) | 2022.02.22 |
| 가우스 소거법, 동차 선형 시스템 (0) | 2022.02.22 |