-벡터 공간의 개념-
벡터 공간(vector space)은 벡터의 덧셈과 스칼라 곱이 정의된 공간을 의미한다. 벡터 공간은 다른 말로 선형 공간(linear space)라고도 부른다. 그러나 벡터 공간에서는 서로 다른 벡터가 서로 다른 길이, 방향을 가질 때 이를 비교할 수 있는 방법이 없다.
길이, 각도와 같은 것이 정의되어 있는 곳은 내적 공간(inner product space)라고 부른다.

흔히 어떤 공간의 좌표 축의 기본 벡터를 유닛 벡터(unit vector)라고 한다.

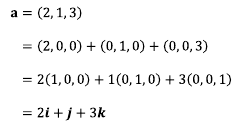
벡터 공간의 일부분을 부분 공간(subspace)라고 한다. 전체 집합과 부분 집합의 관계라고 생각하면 된다. 이런 관계를 설명하는 데에 사용되는 스팬(span)이라는 개념이 있다. 예를 들어, 전체 벡터 공간 V가 3차원이고 2개의 기저 벡터 집합을 S라고 한다. 이때, 집합 S에 속하는 기저 벡터들로 구성되는 2차원 부분 공간을 W라고 했을때, S는 부분 공간 W를 span 한다고 말하고, W=span(S)라고 표현한다.
'Mathematics > Linear algebra' 카테고리의 다른 글
| 기저, 차원 (0) | 2022.02.25 |
|---|---|
| 선형 변환, 선형 독립, 선형 종속 (0) | 2022.02.25 |
| 역행렬의 성질 (0) | 2022.02.25 |
| 역행렬 계산 (0) | 2022.02.25 |
| 행렬식의 성질 (0) | 2022.02.25 |