선형 변환(linear transformation)은 두 벡터 공간 사이의 함수이다. 예를 들어 벡터의 곱 Ax는 벡터 x에 선형 변환 A를 취한 것을 의미한다. 선형 변환은 기존 행렬을 변형시키는 변환이라고 생각할 수 있고 기존 행렬을 다른 좌표 공간으로 이동시킨다고 생각할 수도 있다.


A에 속하는 벡터를 A에 속하는 다른 벡터들의 선형 조합으로 표현할 수 없을 때 A를 선형 독립(linear independent)라고 부른다. 반면, 특정 벡터를 다른 벡터의 선형 조합으로 표현할 수 있다면 선형 종속(linear dependent)라고 한다.
- 선형 독립의 예

위와 같이 A를 구성하는 벡터 a1,a2,a3 모두 다른 벡터의 선형 조합으로 나타낼 수 없다. 따라서 벡터 a1,a2,a3의 집합인 A는 선형 독립이다.

- 선형 종속의 예

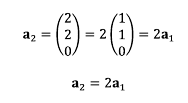

'Mathematics > Linear algebra' 카테고리의 다른 글
| 행 공간, 열 공간, 영 공간, 랭크, 널리티 (0) | 2022.02.25 |
|---|---|
| 기저, 차원 (0) | 2022.02.25 |
| 벡터 공간 (0) | 2022.02.25 |
| 역행렬의 성질 (0) | 2022.02.25 |
| 역행렬 계산 (0) | 2022.02.25 |