1. 삼각 행렬식의 성질
삼각행렬 A의 행렬식은 주 대각 원소의 곱과 같다.
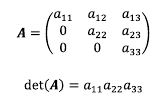
2. 대각 행렬의 행렬식
대각 행렬 A의 행렬식은 삼각 행렬과 마찬가지로 주 대각 원소를 모두 곱한 값과 같다.

단위행렬의 행렬식은 1이다.

3. 전치 행렬의 행렬식

4. 특정 행과 열의 원소가 모두 0일때 행렬식
행렬 A가 정사각 행렬일 때, 행렬 A에 0으로 구성된 행 또는 열이 존재하면 행렬 A의 행렬식은 0이다. 왜냐하면 모든 원소가 0인 행 또는 열을 기준으로 여인수를 구하면 모두 0이기 때문이다.

예를 들어, 위와 같은 행렬 A가 존재할 때 행렬 A의 3열의 원소는 모두 0임을 알 수 있다. 따라서, 행렬 A의 3열을 기준으로 여인수와 행렬식을 구하면 다음과 같다.

5. 행렬의 기본 행 연산과 행렬식
이전에 행렬의 기본 행 연산을 사용할 수 있다는 사실을 공부했는데 기존 행렬의 행 연산 수행은 해당 행렬의 행렬식에 어떤 영향을 미칠까?

a. 한 행에 영이 아닌 상수를 모두 곱한다
정사각 행렬 A의 특정 행 또는 열을 k배 한 행렬을 B라고 하면 다음 관계가 성립한다.

위 식을 보면 A의 1행에만 k배를 했을 뿐인데 전체 행렬식의 크기가 k배 늘어나는 것을 볼 수 있다. 그렇다면 행렬 A의 모든 구성 원소에 k배를 하면 행렬식은 다음과 같이 된다.

모든 구성 원소에 k배를 하면 전체 행렬식은 k의 n승 배가 된다는 것을 알 수 있다.
b. 두 행을 교환한다.
정사각 행렬 A의 두 행 또는 두 열을 교환해서 만든 행렬을 B라고 하면 다음과 같은 관계가 성립한다.
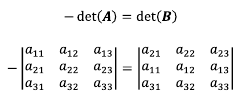
행렬 A의 1행과 2행의 위치를 바꾸면 기존 행렬의 행렬식에서 부호를 바꾼 값과 동일하다는 것을 알 수 있다.
c. 한 행의 배수를 다른 행에 더한다.
정사각 행렬 A의 하나의 행 또는 열의 배수를 다른 행에 더해서 만든 행렬을 행렬 B라고 하면 다음과 같은 관계가 성립한다.
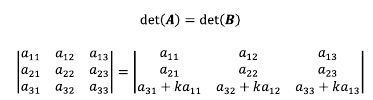
A의 1행에 배를 한후 3행에 더해서 만든 B의 행렬식은 기존 행렬A의 행렬식 값과 동일하다.
6. 비례하는 행과 열에 대한 행렬식
정사각행렬 A에 서로 비례하는 두 행 또는 두 열이 존재한다면 해당 정사각 행렬의 행렬식은 0이다.

7. 행렬 곱과 행렬식

넘파이를 이용해 행렬식을 구해 보자
import numpy as np
A=np.array([[3,2,0],[-1,-3,6],[2,3,-5]])
detA=np.linalg.det(A)
print(detA) #5.000000000000002
'Mathematics > Linear algebra' 카테고리의 다른 글
| 역행렬의 성질 (0) | 2022.02.25 |
|---|---|
| 역행렬 계산 (0) | 2022.02.25 |
| 행렬식의 계산 (0) | 2022.02.22 |
| 가우스 소거법, 동차 선형 시스템 (0) | 2022.02.22 |
| 기본 행 연산, 가우스 조르단 소거법 (0) | 2022.02.21 |