기본 행 연산법
1. 한 행에 영이 아닌 상수를 모두 곱한다.
2. 두 행을 교환한다.
3. 한 행의 배수를 다른 행에 더한다.
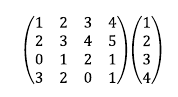
위 첨가행렬을 통해 행 연산에 대해 알아보자.
1. 한 행에 0이 아닌 상수를 모두 곱한다.
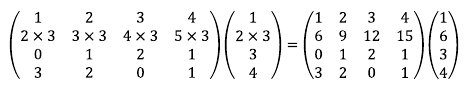
2. 두 행을 교환한다.
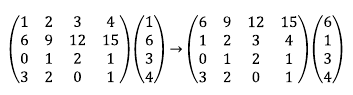
3. 한 행의 배수를 다른 행에 더한다.
한 행의 배수를 다른 행에 더한다는 말의 의미는 첨가 행렬의 한 행에 배수를 구한 후 다른 행에 더하는 것을 의미한다. 예를 들어, 앞서 구한 첨가 행렬에서 2행에 -3을 곱한후 4행에 더하면 다음과 같다.
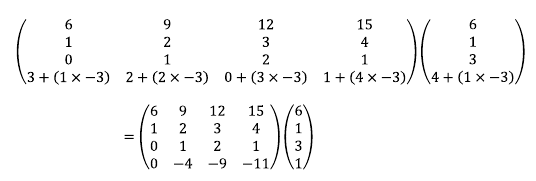
가우스 조르단 소거법
첨가 행렬의 1행 1열 구성 원소를 1로 변형시킨다. 그리고 1행 1열 아래에 위치하는 원소가 0이 되게끔 기본 행 연산을 수행한다. 이와 비슷한 방법으로 나머지 열도 수행한 결과, 다음과 같이 각 행의 가장 첫 원소는 1이고 1아래에 위치하는 원소는 모두 0인 행렬을 가우스 행렬(Gauss matrix)이라고 부른다.
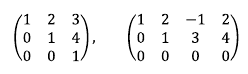
위와 같이 행렬의 구성 원소가 사다리꼴 형태로 남은 것을 가우스 행렬이라고 부른다.
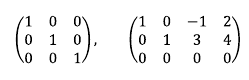
그리고 위와 같이 가장 첫 원소가 1인 열에 대해 1을 제외한 나머지 행 원소가 모두 0인 형태를 기약 가우스 행렬 이라고 부른다.
기약 가우스 행렬 형태를 이용해 방정식의 해를 구하는 방법을 가우스 조르단 소거법이라고 부른다.
<방법>
1. 다음과 같이 식을 첨가 행렬의 형태로 정리한다.
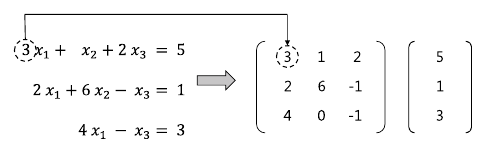
2. 선형 시스템의 첨가 행렬을 구한다.
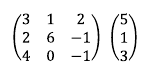
3. 1행에 1/3을 곱한다. 1행에 1/3을 곱하는 이유는 1행 1열 원소를 1로 만들기 위함이다.
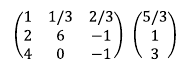
4. 1행에 -2를 곱한후 2행에 더한다. 2행 1열 원소를 0으로 변경하기 위함이다.
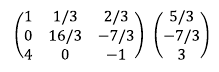
5. 1행에 -4을 곱한 후 3행에 더한다. 3행 1열 원소인 4를 0으로 만들기 위함이다.
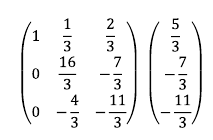
6. 2행에 3/16을 곱한다. 2행 2열 구성 원소를 1로 만들기 위해 자기 자신의 역수를 곱하는 과정이다.
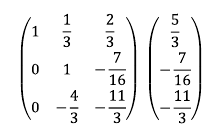
7. 유리수 계산은 번거로우므로, 계산의 편의를 위해 3행에 3을 곱한다.
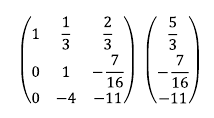
8. 2행에 4를 곱한 후 3행에 더한다. 3행 2열 원소를 0으로 만들기 위해 3행 2열의 음수인 4를 곱하는 것이다.
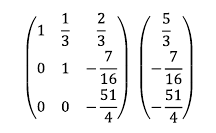
9. 3행에 -4/51을 곱한다. 이를 통해 3행 3열 구성 원소를 1로 만들 수 있다.
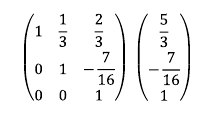
위 첨가 행렬을 보면 첨가 행렬이 가우스 행렬의 형태를 띠는 것을 확인할 수 있다.
10. 2행에 -1/3을 곱한 후 1행에 더한다. 1행 2열 원소를 0으로 만들기 위함이다.
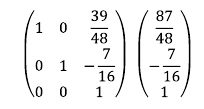
11. 3행에 7/16을 곱한 후 2행에 더한다. 이는 2행 3열 원소를 0으로 만들기 위함이다.
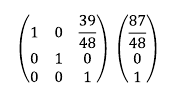
12. 3행에 -39/48을 곱한 후 1행에 더한다. 1행 3열 원소를 0으로 만들기 위함이다.
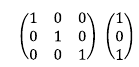
위 첨가 행렬을 보면 기약 가우스 행렬의 형태가 된 것을 확인할 수 있다. 위 첨가 행렬을 다시 선형 시스템으로 표현하면 해를 구할 수 있다.
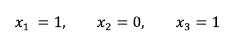
'Mathematics > Linear algebra' 카테고리의 다른 글
| 행렬식의 계산 (0) | 2022.02.22 |
|---|---|
| 가우스 소거법, 동차 선형 시스템 (0) | 2022.02.22 |
| 삼각 행렬, 토플리츠 행렬, 이중 대각 행렬, 하우스홀더 행렬 (0) | 2022.02.21 |
| 대각 행렬, 단위 행렬 (0) | 2022.02.21 |
| 전치 행렬, 대칭 행렬 (0) | 2022.02.21 |