이번에는 선형 시스템의 첨가 행렬을 가우스 행렬로 변환한 후 해를 구하는 방법인 가우스 소거법(Gaussian elimination)을 사용해 해를 구해보겠다.

가우스소거법을 활용해 위 선형 시스템의 해를 구해 보겠다.
1. 첨가 행렬을 구한다.

2. 2행에 1행을 더해 준다. 이는 2행 1열 원소를 0으로 만들기 위함이다.
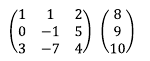
3. 1행에 -3을 곱한 후 3행에 더해준다. 이는 3행 1열 원소를 0으로 만들기 위함이다.

4. 2행에 -1을 곱한다. 이는 2행 2열 원소를 1로 만들기 위함이다.

5. 2행에 10을 곱한 후 3행에 더해 준다. 이는 3행 2열 원소를 0으로 만들기 위함이다.

6. 3행을 -52로 나눈다. 이로써 가우스 행렬을 구했다. 행렬 구성 원소가 사다리꼴 형태인 것을 확인할 수 있다.
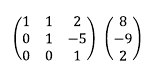
7. 위 첨가 행렬을 다시 선형 시스템으로 표현한 후 해를 구한다.

선형 시스템의 우변이 모두0이면 해당 선형 시스템을 동차 선형 시스템이라고 부른다.

동차 선형 시스템에서는 해가 존재하지 않는 경우는 없다. 즉, 적어도 하나의 해가 존재한다는 의미이다. 왜냐하면 동차 선형 시스템의 선형 방정식은 상수항이 0이므로 다음과 같은 두가지 경우만 존재한다.

방정식의 개수보다 변수의 개수가 많은 동차 선형 시스템은 항상 무한개의 해를 갖는다.
import numpy as np
X=np.array([[3,1,2],[2,6,-1],[4,0,-1]])
y=np.array([[5],[1],[3]])
sol=np.linalg.solve(X,y)
print(sol)
'''
[[1.]
[0.]
[1.]]
''''Mathematics > Linear algebra' 카테고리의 다른 글
| 행렬식의 성질 (0) | 2022.02.25 |
|---|---|
| 행렬식의 계산 (0) | 2022.02.22 |
| 기본 행 연산, 가우스 조르단 소거법 (0) | 2022.02.21 |
| 삼각 행렬, 토플리츠 행렬, 이중 대각 행렬, 하우스홀더 행렬 (0) | 2022.02.21 |
| 대각 행렬, 단위 행렬 (0) | 2022.02.21 |