상 삼각 행렬(upper triangular maxtrix)은 주 대각 원소 아래쪽에 있는 모든 원소가 0인 정사각 행렬을 의미한다.
하 삼각 행렬은 오른쪽 그림과 같다.


- 삼각 행렬의 성질
1. 삼각 행렬 간 덧셈, 뺄셈, 행렬 곱의 결과는 삼각 행렬이다.
2. 상 삼각 행렬의 전치 행렬은 하 삼각 행렬이며, 하 삼각 행렬의 전치 행렬은 상 삼각 행렬이다.

3. 삼각 행렬의 역행렬 또한 삼각 행렬의 형태를 띤다.
import numpy as np
A=np.array([[1,2,3],[4,5,6],[7,8,9]])
Al=np.tril(A)
print(Al)
'''
[[1 0 0]
[4 5 0]
[7 8 9]]
'''
Au=np.triu(A)
print(Au)
'''
[[1 2 3]
[0 5 6]
[0 0 9]]
'''
토플리츠 행렬(Toeplitz matrix)은 다음과 같은 행렬을 의미한다.
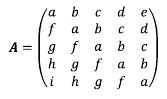

토플리츠 행렬은 시계열 분석을 할 때 자주 사용된다.
이중 대각 행렬(bidiagonal matrix)은 대각 원소뿐만 아니라 대각 원소의 바로 위쪽 혹은 아래쪽 원소가 0이 아닌 행렬이다.
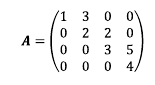
import numpy as np
A=np.array([[1,2,1,3],[5,3,4,1],[2,1,7,9],[2,8,1,3]])
print(A)
'''
[[1 2 1 3]
[5 3 4 1]
[2 1 7 9]
[2 8 1 3]]
'''
diag_ele=np.diag(A)
print(diag_ele) # [1 3 7 3]
print(np.diag(diag_ele))
'''
[[1 0 0 0]
[0 3 0 0]
[0 0 7 0]
[0 0 0 3]]
'''
u_diag_ele=np.diag(A,k=1)
print(u_diag_ele) # [2 4 9], k=1 -> 대각 원소 1칸 위에 있는 원소를 추출한다는 뜻
print(np.diag(u_diag_ele,k=1))
'''
[[0 2 0 0]
[0 0 4 0]
[0 0 0 9]
[0 0 0 0]]
'''
u_diag=np.diag(diag_ele) + np.diag(u_diag_ele,k=1)
print(u_diag)
'''
[[1 2 0 0]
[0 3 4 0]
[0 0 7 9]
[0 0 0 3]]
'''
하우스홀더 행렬(householder matrix)은 어떤 행렬을 다른 형태로 변환할 때 사용하는 행렬중 하나이다. 하우스 홀더 행렬은 정사각 행렬이며 모든 열이 정규 직교한다는 특징이 있다.




import numpy as np
v=np.array([1,0,2,3]) # v는 행벡터
n=len(v)
print(n)
# outer 함수를 이용해 벡터 v와 자기 자신의 외적 행렬을 구한다 (V)(Vt)
outer_mat=np.outer(v,v)
print(outer_mat)
'''
[[1 0 2 3]
[0 0 0 0]
[2 0 4 6]
[3 0 6 9]]
'''
inner_val=np.inner(v,v)
print(inner_val) #14
I=np.identity(n)
H=I-(2/inner_val) * outer_mat
print(H)
'''
[[ 0.85714286 0. -0.28571429 -0.42857143]
[ 0. 1. 0. 0. ]
[-0.28571429 0. 0.42857143 -0.85714286]
[-0.42857143 0. -0.85714286 -0.28571429]]
''''Mathematics > Linear algebra' 카테고리의 다른 글
| 가우스 소거법, 동차 선형 시스템 (0) | 2022.02.22 |
|---|---|
| 기본 행 연산, 가우스 조르단 소거법 (0) | 2022.02.21 |
| 대각 행렬, 단위 행렬 (0) | 2022.02.21 |
| 전치 행렬, 대칭 행렬 (0) | 2022.02.21 |
| 행렬의 대각합 (0) | 2022.02.21 |