CS STUDY

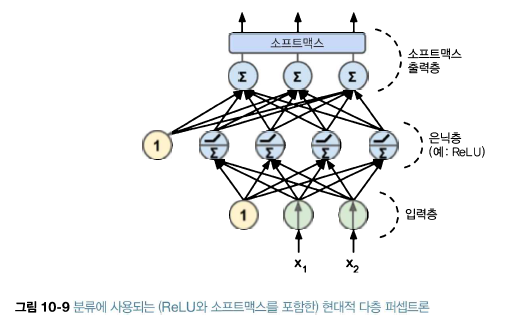
다층 퍼셉트론은 회귀 작업에 사용할 수 있다. 값 하나를 예측하는 데 출력 뉴런이 하나만 필요하다. 이 뉴런의 출력이 예측된 값이다. 다변량 회귀(multivariate regression)에서는 (즉, 동시에 여러 값을 예측하는 경우) 출력 차원마다 출력 뉴런이 하나씩 필요하다. 일반적으로 회귀용 다층 퍼셉트론을 만들 때 출력 뉴런에 활성화 함수를 사용하지 않고 어떤 범위의 값도 출력되도록 한다. 하지만 출력이 항상 양수여야 한다면 출력층에 ReLU 활성화 함수를 사용할 수 있다. 또는 softplus 활성화 함수를 사용할 수 있다. 마지막으로 어떤 범위 안의 값을 예측 하고 싶다면 로지스틱 함수나 하이퍼볼릭 탄젠트 함수를 사용하고 레이블의 스케일을 적절한 범위로 조정할 수 있다. 로지스틱 함수는 0에..

다층 퍼셉트론은 입력층(input layer) 하나와 은닉층(hidden layer) 이라 불리는 하나 이상의 TLU층과 마지막 출력층(output layer)로 구성된다. 입력층과 가까운 층을 보통 하위 층이라 부르고 출력에 가까운 층을 상위 층(upper layer)라고 부른다. 출력층을 제외하고 모든 층은 편향 뉴런을 포함하며 다음 층과 완전히 연결되어 있다. 은닉층을 여러 개 쌓아 올린 인공 신경망을 심층 신경망(deep neural network(DNN)) 이라고 한다. 딥러닝은 심층 신경망을 연구하는 분야이며 조금 더 일반적으로는 연산이 연속하게 길게 연결된 모델을 연구한다. 역전파 알고리즘은 효율적인 기법으로 그레이디언트를 자동으로 계산하는 경사 하강법이다. 네트워크를 두 번 통과하는 것만으..

인공 뉴런 모델은 하나 이상의 이진(on/off) 입력과 이진 출력 하나를 가진다. 인공 뉴런은 단순히 입력이 일정 개수만큼 활성화되었을 때 출력을 내보낸다. 이 네트워크가 어떤 일을 하는지 알아보자. 퍼셉트론(perception)은 가장 간단한 인공 신경망 구조 중 하나로 퍼셉트론은 TLU(threshold logic unit) 또는 이따금 LTU(linear threshold unit)라고 불리는 조금 다른 형태의 인공 뉴런을 기반으로 한다. 입력과 출력이 (이진 on/off 값이 아닌) 어떤 숫자이고, 각각의 입력 연결은 가중치와 연관되어 있다. TLU는 입력의 가중치 합을 계산 한 뒤 계산된 합에 계단 함수(step function)을 적용하여 결과를 출력한다. 즉, h(x)=step(z), 여기..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. CNN을 구성하는 합성곱 계층은 입력으로 받은 이미지를 데이터에서 '무엇으로 보고 있는' 걸까? 이번 절에서는 합성곱 계층을 시각화해서 CNN이 보고있는 것이 무엇인지 알아보도록 하겠다. 1. 1번째 층의 가중치 시각화 하기 앞에서 MNIST 데이터셋으로 간단한 CNN 학습을 해보았는데, 그때 번째 층의 합성곱 계층의 가중치는 그 형상이 (30,1,5,5) 였다. (필터 30개, 채널 1개, 5x5크기). 필터의 크기가 5x5이고 채널이 1개라는 것은 이 필터를 1채널의 회색조 이미지로 시각화할 수 있다는 뜻이다. 그럼 합성곱 계층(1층째) 필터를 이미지로 나타내보자. 학습전 필터는 무작위로 초기화되고 있어 흑백의 정도에 규칙성이 없다...

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. class SimpleConvNet: def __init__ (self,input_dim=(1,28,28),conv_param={'filter_num':30,'filter_size':5, 'pad':0,'stride':1}, hidden_size=100,output_size=10,weight_init_std=0.01): filter_num=conv_param['filter_num'] filter_size=conv_param['filter_size'] filter_pad=conv_param['pad'] filter_stride=conv_param['stride'] input_size=input_dim[1] conv_output_size=(..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 1. 4차원 배열 CNN에서 계층 사이를 흐르는 데이터는 4차원이다. 예를 들어 데이터의 형상이 (10,1,28,28)이면, 이는 높이 28,너비 28, 채널 1개인 데이터가 10개라는 이야기이다. 2. im2col로 데이터 전개하기 im2col은 입력 데이터를 필터링(가중치 계산) 하기 좋게 전개하는 함수이다. 아래 그림과 같이 3차원 입력 데이터에 im2col을 적용하면 2차원 행렬로 바뀐다. 정확히는 배치 안의 데이터 수까지 포함한 4차원 데이터를 2차원으로 변환한다. 위 그림에서는 보기 좋게끔 스트라이드를 크게 잡아 필터의 적용 영역이 겹치지 않도록 했지만, 실제 상황에서는 영역이 겹치는 경우가 대부분이다. 필터 적용 영역이 겹치..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 풀링은 세로, 가로 방향의 공간을 줄이는 연산이다. 위 그림은 최대 풀링(max pooling)을 스트라이드 2로 처리하는 순서이다. -풀링 계층의 특징- 1) 학습해야 할 매개변수가 없다 2) 채널 수가 변하지 않는다 3) 입력의 변화에 영향을 적게 받는다

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. CNN에서는 패딩(padding), 스트라이드(stride)등 CNN 고유의 용어가 등장한다. 또, 각 계층 사이에는 3차원 데이터같이 입체적인 데이터가 흐른다는 점에서 완전연결 신경망과 다르다. 1. 완전연결 계층의 문제점 완전연결 계층의 문제점은 바로 데이터의 형상이 무시된다는 사실이다. 입력 데이터가 이미지인 경우를 예로 들면, 이미지는 통상 가로,세로,채널(색상)로 구성된 3차원 데이터이다. 그러나 완전연결 계층에 입력할 때는 3차원 데이터를 평평한 1차원 데이터로 평탄화해줘야 한다. 사실 지금까지의 MNIST 데이터셋을 사용한 사례에서는 형상이 (1,28,28)인 이미지 (1채널, 세로 28픽셀, 가로 28픽셀)를 1줄로 세운 ..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다, CNN도 지금까지 본 신경망과 같이 레고 블록처럼 계층을 조합하여 만들 수 있다. 다만, 합성곱 계층(convolutional layer)과 폴링 계층(pooling layer)이 새롭게 등장한다. 지금까지 본 신경망은 인접하는 계층의 모든 뉴런과 결합되어 있었다. 이를 완전연결(fully connected)이라고 하며, 완전히 연결된 계층을 Affine 계층이라는 이름으로 구현했다. 이 Affine 계층을 사용하면, 가령 층이 5개인 완전연결 신경망은 다음 그림과 같이 구현할 수 있다. CNN의 구조는 다음과 같다. 위 그림과 같이 CNN에서는 새로운 합성곱 계층(Conv)와 풀링 계층(pooling)이 추가된다.

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 신경망에는 하이퍼파라미터가 다수 등장한다. 여기서 말하는 하이퍼파라미터는 각 층의 뉴런 수, 배치 크기, 매개변수 갱신 시의 학습률과 가중치 감소 등이다. 이러한 하이퍼파라미터 값을 적절히 설정하지 않으면 모델의 성능이 크게 떨어지기도 한다. 하이퍼파라미터의 값은 매우 중요하지만 그 값을 결정하기까지는 일반적으로 많은 시행착오를 겪는다. 이번 절에서는 하이퍼파라미터의 값을 최대한 효율적으로 탐색하는 방법을 설명한다. 1. 검증 데이터 하이퍼파라미터의 성능을 평가할 때는 시험 데이터를 사용해서 안 된다. 왜냐하면 시험 데이터를 사용하여 하이퍼파라미터를 조정하면 하이퍼파라미터 값이 시험 데이터에 오버피팅 되기 때문이다. 하이퍼파라미터 조정용..