이번 포스팅에서는 Aggregated Residual Transformations for Deep Neural Network논문에 소개된 ResNeXt에 대해서 정리해 보겠다.
이 network는 동일한 위상을 가진 일련의 변환을 집계하는 빌딩 블록을 반복하여 구성된다. 간단한 설계 덕분에 설정할 하이퍼 파라미터가 몇 개에 불과한 동종 멀티 브랜치 구조가 구축된다.
ResNext 모델은 2016 ILSVRC 에서 1st Runner를 달성했다.

1. Aggregated Transformation
우리가 이미 알듯이 간단한 neuron은 아래 그림과 같다.
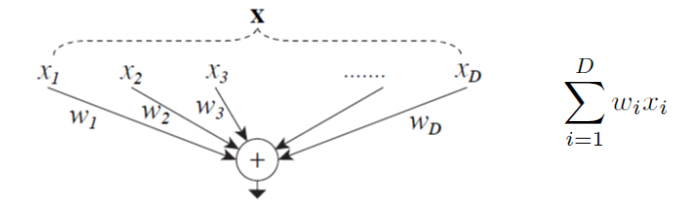
이 모델에서의 주된 특징 중 하나는 Aggregated Transformation이다.
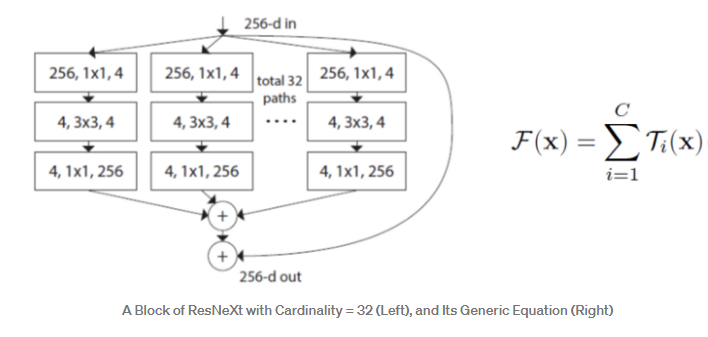
Network in Network와 반대로 Network in Neuron이라고 하는데 이는 차원을 늘리는 효과를 가져다 준다. 간단한 뉴런에는 선형함수가 wi 와 xi 가 곱해지는것 대신에 비선형 함수가 각각의 통로에 수행된다.
새로운 dimension인 C가 논문에서 소개되어지는데 이는 Cardinality라고 불린다. cardinality의 치수가 complex transformations의 수를 조절한다.
2. Inception-ResNet, Grouped Convolution in AlexNet, ResNext 비교
논문에 소개된 3가지 모델을 비교해보자.
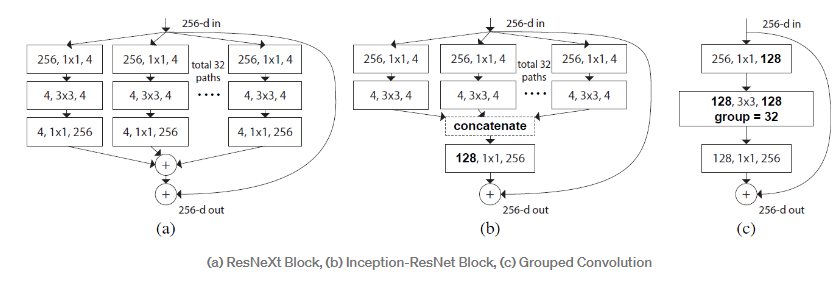
(a). ResNext Block
- 각각의 통로에서 Conv1x1 - Conv3x3 - Conv1x1이 수행된다. 각각의 통로의 internal dimension은 d로 표시한다(d=4). 통로의 수는 cardinality C(C=32)이다.
- dimension은 4에서 부터 256까지 증가하게 된다. 그리고 마지막에 skip connection 통로를 통해 더해진다.
- Inception-ResNet과 비교해보면 각각의 통로를 design하는데 최소한의 추가 작업만 필요하다.
- ResNet과는 달리 한개의 통로는 다른 통로와 연결되지 않는다.
(b). Inception-ResNet Block
- 각각의 통로는 Conv1x1 - Conv3x3이 수행되고 128의 dimension 으로 concatenated된다. 그리고 128로부터 256으로 dimension을 복원하기 위해 Conv1x1이 수행된다.
- skip connection과 더해진다.
- 주된 차이점은 early concatenation이다.
(c). Gropued Convolution in AlexNet
(Grouped Convolution 은 입력 값의 채널들을 여러 개의 그룹으로 나누어 독립적으로 Convolution 연산을 수행하는 방식이다. 이는 아이디어와 구현 방법이 간단하며, 병렬 처리에 유리하다는 장점이 있다.)
- Conv1x1-Conv3x3-Conv1x1이 수행된다. Conv3x3은 128의 dimension을 갖고 있다.
- 그러나 group convolution 이 여기서 사용된다. 그러므로 Conv3x3은 더 넓지만 sparsely connected 되어있다(왜냐하면 하나의 통로에 있는 뉴런들은 다른 통로에 있는 뉴런과 연결되어 있지 않을 것이기 때문이다).
- 그러므로, 여기에서는 32개의 group을 사용한다.
- skip connection이 마지막으로 더해진다.
(b)와 (c)의 구조가 항상 1.2에 나타난 방정식의 일반적인 형태와 동일하지는 않지만, 실제로 저자들은 위와 같이 위의 세 가지 구조를 시도했고, 그들은 결과가 동일하다는 것을 발견했다.
결론적으로 저자들은 (c)가 다른 다른 두 모델보다 간결하고 더 빠르기 때문에 (c)를 선택했다.
구현
def block(input,filter,strides=1):
x=Conv2D(4,(1,1),strides=1,padding='same')(input)
x=BatchNormalization()(x)
x=Activation('relu')(x)
x=Conv2D(4,(3,3),strides=strides,padding='same')(x)
x=BatchNormalization()(x)
x=Activation('relu')(x)
x=Conv2D(filter,(1,1),strides=1,padding='same')(x)
x=BatchNormalization()(x)
x=Activation('relu')(x)
return xdef ResNeXt_a():
input=Input((32,32,3))
x=Conv2D(64,(3,3),strides=1,padding='same')(input)
x=BatchNormalization()(x)
x=Activation('relu')(x)
for i in range(3):
x=total_block(x,64)
x=MaxPool2D((2,2),strides=1,padding='same')(x)
x=Conv2D(128,(3,3),strides=2,padding='same')(x)
x=BatchNormalization()(x)
x=Activation('relu')(x)
for i in range(3):
x=total_block(x,128)
x=MaxPool2D((2,2),strides=1,padding='same')(x)
x=Conv2D(256,(3,3),strides=2,padding='same')(x)
x=BatchNormalization()(x)
x=Activation('relu')(x)
for i in range(3):
x=total_block(x,256)
x=MaxPool2D((2,2),strides=1,padding='same')(x)
x=Flatten()(x)
x=Dense(10,activation='softmax')(x)
return Model(input,x)def total_block(input,filter,strides=1,C=8):
x=input
for i in range(C):
y=block(input,filter,strides)
x=Add()([x,y])
x=Add()([x,input])
return x'논문 리뷰, 구현' 카테고리의 다른 글
| 9. Wide Residual Network 논문 리뷰 (0) | 2022.07.04 |
|---|---|
| 8. SqueezeNet 논문 리뷰, 구현 (0) | 2022.07.03 |
| 7. DenseNet 논문 리뷰,구현 (0) | 2022.07.03 |
| 6. ResNet 논문 리뷰, 구현 (0) | 2022.07.03 |
| 5.Network in Network 논문 리뷰 (0) | 2022.07.03 |