이번 포스팅에서는 Deep Residual Learning for Image Recognition 논문을 리뷰해 보겠다.
Abstract
Deep neural network는 훈련하기 더 어렵다. 논문의 저자들은 residual framework를 이전보다 깊은 network들을 쉽게 훈련시키기 위해 제시했다. 이들은 참조되지 않은 함수를 학습하는 대신 input layer를 기준으로 learning residual functions로 층을 명시적으로 재구성했다.
이들은 포괄적인 경험적 증거를 제공했는데 이러한 residual networks가 최적화 하기 쉽고 상당히 증가된 깊이로부터 accuracy를 얻을수 있다는 것을 보여준다.
ResNet 구조는 ILSVRC 2015에서 1등을 차지했다.
Introduction
신경망의 깊이는 상당히 중요한 역할을 한다. 깊이의 의의에 따라 다음과 같은 의문이 발생한다. 더 나은 네트워크를 배우는 것이 더 많은 계층을 쌓는 것만큼 쉬운가?
이 질문에 답하는데 걸림돌은 처음부터 수렴에 걸림돌이 되는 기울기가 사라지거나 폭발하는 악명 높은 문제였다. 그러나 이 문제는 정규화된 초기화와 수십 개의 계층을 가진 네트워크가 역전파를 통해 확률적 구배 하강(SGD)을 위해 수렴을 시작할 수 있도록 하는 중간 정규화 계층으로 크게 해결되었다.
deeper network가 수렴하기 시작하면, 성능저하 문제가 발생한다. 이 문제는 깊이가 증가하면 정확도가 포화하면서 성능저하가 빨라진다. 이러한 손상은 overfitting에 의해 생긴것이 아니고 더 층을 추가하는것은 더 높은 training error를 이끈다. Fig1이 이에 관련된 그림이다.

이 논문 저자들은 deep residual learning framework를 소개하면서 이 성능 저하 문제를 해결했다. 각각의 stakced layers 가 직접적으로 원하는 기본의 매핑을 fit하는 대신에 이들은 이러한 층들이 residual mapping에 fit 하도록 했다.
Fig(2)의 그림에 나온 F(x) + x 는 'shortcut connetions'라는 feedforward nerual network로 이해될 수 있다. shortcut connection은 하나 또는 그 이상의 층을 스킵하는 것이다.

이 논문에서는 shortcut connections는 단순히 identity mapping을 수행했고, 이들의 output들이 stacked layers의 output에 추가되었다. 이들의 deep residual net은 상당히 증가된 깊이의 신경망에서 쉽게 정확도를 얻을수 있었는데 이는 이전 networks들보다 실질적으로 더 좋았다.
Deep Residual Learning
논문 저자들을 residual learning을 몇몇 stacked 층마다 채택했다. 이 building block는 Fig2에서 확인할 수 있다. 이 논문에서는 building block을 다음과 같이 정의했다.

x,y는 input 과 output 벡터들이다. F(x,{wi})는 훈련 되어져야 할 residual mapping을 나타낸다. 시그마는 ReLU 함수이다. F+X 작업은 shortcut connection과 elementwise addition을 통해 수행된다. 이들은 addition 이후에 second nonlinearity를 채택했다.
Eqn.(1)의 shortcut connection은 추가 매개 변수도 계산 복잡성도 유발하지 않는다.
X와 F의 dimension은 방정식(1)에서 같아야 한다. 그렇지 않은 경우(예: 입력/출력 채널을 변경할 때), 바로 가기 연결을 통해 선형 투영 W를 수행하여 dimension을 일치시킬 수 있다.

또한 방정식(1)의 제곱 행렬 W를 사용할 수 이다. 그러나 우리는 실험을 통해 ID mapping이 성능 저하 문제를 해결하기에 충분하고 경제적이며, 따라서 W는 dimension을 일치시킬 때만 사용됨을 보여준다.
잔차 함수 F의 형태는 유연하다. 본 논문의 실험은 두개 또는 세 개의 층을 갖는 함수 F를 포함하며(Fig 5), 더 많은 층이 가능하다. 그러나 F에 단일 층만 있는 경우 (1)은 선형 층: y=W1x + x와 유사하며, 이로 인해 장점이 관찰되지 않는다.
또한 위의 표기법은 단순성을 위해 완전히 연결된 계층에 대한 것이지만 컨볼루션 층에도 적용할 수 있다. 함수 F(x,{Wi})는 여러 개의 컨볼루션 층을 나타낼 수 있다. 요소별 추가는 채널별 두 특성 맵에서 수행된다.
Network Architectures
논문 저자들은 다양한 plain/residual net을 test 했고, 지속적인 현상을 관찰했다. 이 논의에 대한 instance를 제공하기 위해 이들은 다음과 같은 두가지 모델을 가지고 설명했다.
Plain Network
이들의 plain은 VGG의 철학에 기초했다. 합성곱층 필터는 대부분 3x3 필터는 가지고 있고 두가지 간단한 simple design rules을 가지고 있다.
첫번째는 같은 output feature map size을 위해서, 층들은 같은 수의 필터를 가지고 있다.
두번째는 만약 feature map size가 절반으로 줄어든다면, 필터의 수는 층마다 time complexity를 보존하기 위해 두배가 된다. 이들은 strides=2를 이용했다.
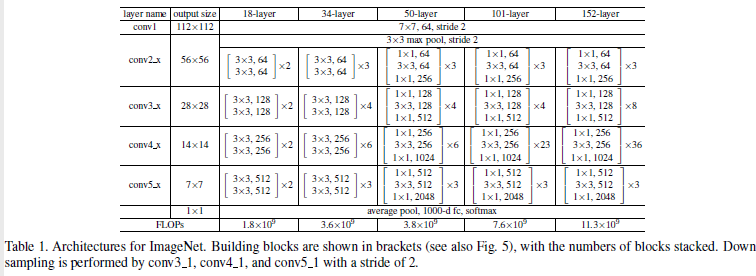
Network는 global average pooling layer와 1000개의 완전연결층(소프트 맥스 함수를 사용한)으로 종료된다. weighted layers의 총 수는 34개이다.
가치있는 점은 이들의 모델은 VGG보다 더 적은 필터와 더 낮은 complexity를 가지고 있다는 점이다.
Residual Network
위에서 소개한 plain network를 기반으로 한다. 이들은 shortcut connection를 주입했는데 이는 네트워크를 counterpart residual version으로 전환한다. identity shortcut은 input 과 output이 같은 차원일때 직접적으로 사용될 수 있다. 차원이 증가하면 두가지 옵션을 고려할 수 있다.
첫번째는 shortcut은 치수 증가를 위해 extra zero 항목을 패딩하여 identity mapping을 수행한다. 이 옵션은 추가 매개 변수를 도입하지 않는다.
두번째는 projection shortcut(식2)로 이는 차원을 맞추는데 사용된다(1x1 convolutions으로 수행된다).
이 두가지 옵션은 shortcut이 두가지 사이즈의 feature map으로 갈때, 이들은 stride=2로 수행된다.


Implementation
이미지 크기는 scale augmentation을 위해 [256,480]에서 무작위로 샘플링된 짧은 면과 함께 조정된다. 224x224 crop에서는 픽셀당 평균을 뺀 이미지 또는 수평 플립에서 무작위로 샘플링된다. 표준 color augmentation이 사용되었다.
이들은 batchnormalization을 사용했는데 이 층은 각각의 convolution 이후와 활성화 함수 이전 사이에 사용되었다. SGD와 256 미니배치를 사용했다.
error가 정제되었을때 학습률은 0.1부터 10분의1씩 작아졌고 60x10^4 반복만큼 훈련되었다. 이들은 weight decay=0.0001 그리고 momentum=0.9를 사용했다. 이들은 dropout 을 사용하지 않았다.
ResNet50 구현
def resnet_identity(x,filters):
#차원이 변하지 않는 block
#we will have 3 blocks and then input will be added
x_skip=x
f1,f2=filters
# first block
x=Conv2D(f1,(1,1),1,padding='valid',kernel_regularizer=keras.regularizers.l2(0.001))(x)
x=BatchNormalization()(x)
x=Activation(keras.activations.relu)(x)
# second block
x=Conv2D(f1,(3,3),1,padding='same',kernel_regularizer=keras.regularizers.l2(0.001))(x)
x=BatchNormalization()(x)
x=Activation(keras.activations.relu)(x)
# third block
x=Conv2D(f2,(1,1),1,padding='valid',kernel_regularizer=keras.regularizers.l2(0.001))(x)
x=BatchNormalization()(x)
x=Add()([x,x_skip])
x=Activation(keras.activations.relu)(x)
return xfrom keras.regularizers import L2
def resnet_conv(x,s,filters):
# input 의 차원이 1x1 convolution과 stride=2에 의해 바뀌게 된다.
# 그러므로 skip connection도 차원 변화를 처리해줘야 한다.
x_skip=x
f1,f2=filters
# first block
x=Conv2D(f1,(1,1),s,padding='valid',kernel_regularizer=keras.regularizers.l2(0.001))(x)
x=BatchNormalization()(x)
x=Activation(keras.activations.relu)(x)
# second block
x=Conv2D(f1,(3,3),1,padding='same',kernel_regularizer=keras.regularizers.l2(0.001))(x)
x=BatchNormalization()(x)
x=Activation(keras.activations.relu)(x)
# thrid block
x=Conv2D(f2,(1,1),1,padding='valid',kernel_regularizer=keras.regularizers.l2(0.001))(x)
# shortcut
x_skip=Conv2D(f2,(1,1),s,padding='valid',kernel_regularizer=keras.regularizers.l2(0.001))(x_skip)
x_skip=BatchNormalization()(x_skip)
# add
x=Add()([x,x_skip])
x=Activation(keras.activations.relu)(x)
return xfrom keras.layers.convolutional import ZeroPadding2D
def resnet50():
input_im=Input(shape=(224,224,3))
x=ZeroPadding2D(padding=(3,3))(input_im)
# 1st stage
x=Conv2D(64,(7,7),2)(x)
x=BatchNormalization()(x)
x=Activation(keras.activations.relu)(x)
x=MaxPool2D((3,3),2)(x)
# 2nd stage
x=resnet_conv(x,1,(64,256))
x=resnet_identity(x,(64,256))
x=resnet_identity(x,(64,256))
# 3rd stage
x=resnet_conv(x,2,(128,512))
x=resnet_identity(x,(128,512))
x=resnet_identity(x,(128,512))
x=resnet_identity(x,(128,512))
#4th stage
x=resnet_conv(x,2,(256,1024))
x=resnet_identity(x,(256,1024))
x=resnet_identity(x,(256,1024))
x=resnet_identity(x,(256,1024))
x=resnet_identity(x,(256,1024))
x=resnet_identity(x,(256,1024))
# 5th stage
x=resnet_conv(x,2,(512,2048))
x=resnet_identity(x,(512,2048))
x=resnet_identity(x,(512,2048))
x=AvgPool2D((7,7))(x)
x=Flatten()(x)
x=Dense(1000,activation='softmax',kernel_initializer='he_normal')(x)
model=Model(inputs=input_im,outputs=x,name='Resnet50')
return model'논문 리뷰, 구현' 카테고리의 다른 글
| 8. SqueezeNet 논문 리뷰, 구현 (0) | 2022.07.03 |
|---|---|
| 7. DenseNet 논문 리뷰,구현 (0) | 2022.07.03 |
| 5.Network in Network 논문 리뷰 (0) | 2022.07.03 |
| 4.GoogleNet 논문 리뷰, 구현 (0) | 2022.06.29 |
| 3.VGG 논문 리뷰,구현 (0) | 2022.06.29 |