선형 SVM 분류기가 효율적이고 많은 경우에 아주 잘 작동하지만, 선형적으로 분류할 수 없는 데이터셋이 많다. 비선형 데이터셋을 다루는 한 가지 방법은 다항 특성과 같은 특성을 더 추가하는 것이다. 이렇게 하면 선형적으로 구분되는 데이터셋이 만들어질 수 있다. 왼쪽 그래프는 하나의 특성 x1만을 가진 간단한 데이터셋을 나타낸다. 그림에서 볼 수 있듯이 이 데이터셋은 선형적으로 구분이 안 된다. 하지만 두 번째 특성 x2=(x1)^2을 추가하여 만들어진 2차원 데이터셋은 완벽하게 선형적으로 구분할 수 있다.

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
X,y=make_moons(n_samples=100,noise=0.15)
polynomial_svm_clf=Pipeline([
('poly_features',PolynomialFeatures(degree=3)),
('scaler',StandardScaler()),
('svm_clf',LinearSVC(C=10,loss='hinge'))
])
polynomial_svm_clf.fit(X,y)
SVM을 사용할 땐 커널 트릭 이라는 거의 기적에 가까운 수학적 기교를 적용할 수 있다. 커널 트릭은 실제로는 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있다. 사실 어떤 특성도 추가하지 않기 때문에 엄청난 수의 특성 조합이 생기지 않는다.
from sklearn.svm import SVC
poly_kernel_svm_clf=Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='poly',degree=3,coef0=1,C=5))
])
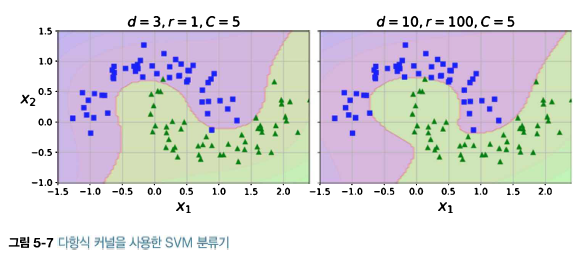
poly_kernel_svm_clf.fit(X,y)이 코드는 3차 다항식 커널을 사용해 SVM 분류기를 훈련시킨다. 결과는 다음 그림 왼쪽에 나타나 있다. 오른쪽 그래프는 10차 다항식 커널을 사용한 또 다른 SVM 분류기이다. 모델이 과대적합이라면 다항식의 차수를 줄여야 한다. 반대로 과소적합이라면 차수를 늘려야 한다. 매개변수 coef0는 모델이 높은 차수와 낮은 차수에 얼마나 영향을 받을지 조절한다.
비선형 특성을 다루는 또 다른 기법은 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정하는 유사도 함수로 계산한 특성을 추가하는 것이다.

예를 들어서 앞에서 본 1차원 데이터셋에 두개의 랜드마크 x1=-2와 x1=1을 추가하자(그림 5-8의 왼쪽 그래프). 그리고 r=0.3인 가우시안 방사 기저 함수(RBF)를 유사도 함수로 정의하겠다.
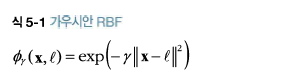

랜드마크를 선택하는 간단한 방법은 데이터셋에 있는 모든 샘플 위치에 랜드마크를 설정하는 것이다. 이렇게 하면 차원이 매우 커지고 따라서 변환된 훈련 세트가 선형적으로 구분될 가능성이 높다. 단점은 훈련 세트에 있는 n개의 특성을 가진 m개의 샘플이 m개의 특성을 가진 m개의 샘플로 변환된다는 것이다(원본 특성은 제외한다고 가정한다). 훈련 세트가 매우 클 경우 동일한 크기의 아주 많은 특성이 만들어진다.
다항 특성 방식과 마찬가지로 유사도 특성 방식도 머신러닝 알고리즘에 유용하게 사용될 수 있다. 추가 특성을 모두 계산하려면 연산 비용이 많이 드는데 특히 훈련 세트가 클 경우 더 그렇다. 여기에서 커널 트릭이 한 번 더 SVM의 마법을 만든다. 유사도 특성을 ㅁ낳이 추가하는 것과 같은 비슷한 결과를 얻을 수 있다. 가우시안 RBF 커널을 사용한 SVC 모델을 시도해보자.
rbf_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='rbf',gamma=5,C=0.01))
])
rbf_kernel_svm_clf.fit(X,y)
gamma(r)를 증가시키면 종 모양 그래프가 좁아져서 각 샘플의 영향 범위가 작아진다. 결정 경계가 조금 더 불규칙해지고 각 샘플을 따라 구불구불하게 휘어진다. 반대로 작은 gamma 값은 넓은 종 모양 그래프를 만들며 샘플이 넓은 범위에 걸쳐 영향을 주므로 결정 경계가 더 부드러워진다. 하이퍼파라미터 r이 규제 역할을 한다. 모델이 과대적합일 경우엔 감소시켜야 하고 과소적합일 경우에는 증가시켜야 한다 (하이퍼파라미터 C와 비슷하다).

<계산 복잡도>
LinearSVC 는 커널 트릭을 지원하지 않지만 훈련 샘플과 특성 수에 거의 선형적으로 늘어난다. 이 알고리즘의 훈련 시간 복잡도는 대략 O(mxn) 정도이다.
정밀도를 높이면 알고리즘의 수행 시간이 길어진다. 이는 허용오차 하이퍼파라미터 e으로 조절한다(사이킷런에서는 매개변수 tol이다). 대부분의 분류 문제는 허용오차를 기본값으로 두면 잘 작동한다.
SVC는 훈련의 시간 복잡도는 보통 O(m^2xn)과 O(m^3xn) 사이이다. 이는 훈련 샘플 수가 커지면 엄청나게 느려진다는 것을 의미한다. 복잡하지만 작거나 중간 규모의 훈련 세트에 이 알고리즘이 잘 맞는다. 하지만 특성의 개수에는, 특히 희소 특성(즉, 각 샘플에 0이 아닌 특성이 몇개 없는 경우)인 경우에는 잘 확장된다. 이런 경우 알고리즘의 성능이 샘플이 가진 0이 아닌 특성의 평균 수에 거의 비례한다.

'Machine Learning > Advanced (hands on machine learning)' 카테고리의 다른 글
| 16. 결정 트리 - 결정 트리 학습과 시각화, 예측 (0) | 2021.05.21 |
|---|---|
| 14. 서포트 벡터 머신 - SVM 회귀 (0) | 2021.05.20 |
| 12. 서포트 벡터 머신 - 선형 SVM 분류 (0) | 2021.05.19 |
| 11. 모델 훈련 - 로지스틱 회귀 (0) | 2021.05.19 |
| 10. 모델훈련 - 규제가 있는 선형 모델 (0) | 2021.05.19 |