과대적합을 감소시키는 좋은 방법은 모델을 규제하는 것이다. 다항 회귀 모델을 규제하는 간단한 방법은 다항식의 차수를 감소시키는 것이다.
선형 회귀 모델에서는 보통 모델의 가중치를 제한함으로써 규제를 가한다. 각기 다른 방법으로 가중치를 제한하는 '릿지'회귀, '라쏘'회귀, 엘라스틱넷을 살펴보겠다.
<릿지 회귀>
릿지 회귀는 규제가 추가된 선형 회귀 버전이다. 규제항이 비용함수에 추가된다.

다음 그림은 선형 데이터에 몇 가지 다른 a를 사용해 릿지 모델을 훈련시킨 결과이다.

a를 증가시킬수록 직선에 가까워지는 것을 볼 수 있다. 즉, 모델의 분산을 줄지만 편향은 커지게 된다.


from sklearn.linear_model import Ridge
ridge_reg=Ridge(alpha=1,solver='cholesky')
ridge_reg.fit(X,y)
ridge_reg.predict([[1.5]])
다음은 확률적 경사 하강법을 사용했을 때이다.
seg_reg=SGDRegressor(penalty='l2')
sgd_reg.fit(X,y.ravel())
sgd_reg.predict([[1.5]])
penalty 매개변수는 사용할 규제를 지정한다. 'l2'는 SGD가 비용 함수에서 가중치 벡터의 l2노름의 제곱을 2로 나눈 규제항을 추가하게 만든다. 즉, 릿지 회귀와 같다.
<라쏘 회귀>
라쏘 회귀는 선형 회귀의 또 다른 규제된 버전이다. 릿지 회귀처럼 비용 함수에 규제항을 더하지만 l2노름의 제곱을 2로 나눈 것 대신 가중치 백터의 l1노름을 사용한다.

다음 그림은 위에 4-17과 같지만 더 작은 a값을 사용했다.
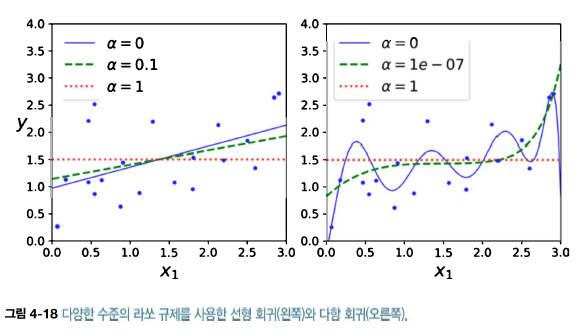
라쏘 회귀의 중요한 특징은 덜 중요한 특성의 가중치를 제거하려고 한다는 점이다.(즉, 가중치가 0이 된다). 라쏘 회귀는 자동으로 특성 선택을 하고 희소 모델(sparse model)을 만든다. 즉, 0이 아닌 특성의 가중치가 적다.



다음은 Lasso 클래스를 사용한 간단한 사이킷런 예제이다.
from sklearn.linear_model import Lasso
lasso_reg=Lasso(alpha=0.1)
lasso_reg.fit(X,y)
lasso_reg.predict([[1.5]])

Lasso 대신 SGDRegressor (penalty='l1')을 사용할 수도 있다.
<엘라스틱넷>
엘라스틱넷은 릿지 회귀와 라쏘 회귀를 절충한 모델이다.
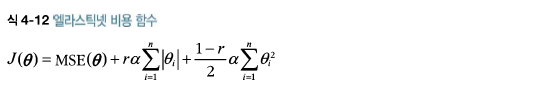

그럼 보통의 선형 회귀(즉, 규제가 없는 모델), 릿지, 라쏘, 엘라스틱넷을 언제 사용해야 할까? 적어도 규제가 약간 있는것이 대부분의 경우에 좋으므로 일반적으로 평범한 선형 회귀는 피해야 한다. 릿지가 기본이 되지만 쓰이는 특성이 몇 개뿐이라고 의심되면 라쏘나 엘라스틱넷이 낫다. 특성 수가 훈련 샘플보다 많거나 특성 몇 개가 강하게 연관되어 있을 때는 보통 라쏘가 문제를 일으키므로 라쏘보다는 엘라스틱넷을 선호한다.
다음은 사이킷런의 ElasticNet을 사용한 간단한 예제이다(lr_ratio가 혼합 비율 r이다).
from sklearn.linear_model import ElasticNet
elastic_net=ElasticNet(alpha=0.1,l1_ratio=0.5)
elastic_net.fit(X,y)
elastic_net.predict([[1.5]])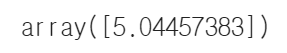
'Machine Learning > Advanced (hands on machine learning)' 카테고리의 다른 글
| 12. 서포트 벡터 머신 - 선형 SVM 분류 (0) | 2021.05.19 |
|---|---|
| 11. 모델 훈련 - 로지스틱 회귀 (0) | 2021.05.19 |
| 9. 모델 훈련 - 학습 곡선 (0) | 2021.05.18 |
| 8. 모델훈련 - 다항 회귀 (0) | 2021.05.18 |
| 7. 모델훈련 - 경사하강법 (0) | 2021.05.18 |