CS STUDY

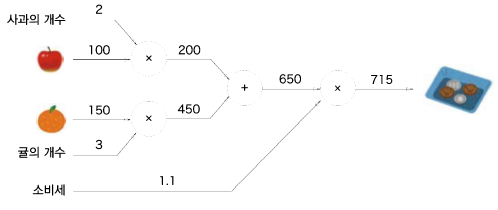
이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 1. 신경망 학습의 전체 그림 지금까지 설명한 오차역전파법이 등장하는 단계는 두 번째인 '기울기 산출' 이다. 앞에서는 기울기를 구하기 위해서 수치 미분을 사용했는데 수치 미분은 구현하기 쉽지만 계산이 오래걸렸다. 오차역전파법을 이용하면 느린 수치 미분과 달리 기울기를 효율적이고 빠르게 구할 수 있다. 2. 오차역전파법을 적용한 신경망 구현하기 import sys,os sys.path.append(os.pardir) import numpy as np from common.layers import * from common.gradient import numerical_gradient from collections import Ordered..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 1. ReLU 계층 활성화 함수로 사용되는 ReLU의 수식은 다음과 같다. 바로 위의 식과 같이 순전파 때의 입력인 x가 0보다 크면 역전파는 상류의 값을 그대로 하류로 흘린다. 반면, 순전파 때 x가 0 이하면 역전파 때는 하류로 신호를 보내지 않는다. (0을 보낸다). 계산 그래프로는 다음처럼 그릴 수 있다. 이제 이 ReLU 계층을 구현해보자. 신경망 계층의 forward() 와 backward() 함수는 넘파이 배열을 인수로 받는다고 가정하자. class Relu: def __init__ (slef): self.mask=None def forward(self,x): self.mask=(x

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 이번 장에서는 가중치 매개변수의 기울기를 효율적으로 계산하는 오차역전파법(backpropagation)을 공부한다. 1. 계산 그래프 다음 문제를 계산 그래프로 나타내보자. 문제: 현빈 군은 슈퍼에서 사과를 2개, 귤을 3개 샀다. 사과는 1개에 100원, 귤은 1개 150원 이다. 소비세가 10%일 때 지불 금액을 구하라. 계산을 왼쪽에서 오른쪽으로 진행하는 단계를 순전파라고 한다. 순전파는 계산 그래프의 출발점부터 종착점으로의 전파이다. 오른쪽에서 왼쪽 방향으로의 전파는 역전파라고 한다. 역전파는 이후에 미분을 계산할 때 중요한 역할을 한다. 계산 그래프의 특징은 '국소적 계산' 을 전파함으로써 최종 결과를 얻는다는 점에 있다. 계산..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 학습 알고리즘 구현하기 신경망 학습의 절차는 다음과 같다. 이는 경사 하강법으로 매개변수를 갱신하는 방법이며, 이때 데이터를 미니배치로 무작위로 선정하기 때문에 확률적 경사 하강법(stochastic gradient descent, SGD) 라고 부른다. 그럼 실제로 손글씨 숫자를 학습하는 신경망을 구현해보자. 여기에서는 2층 신경망(은닉층이 1개인 네트워크)를 대상으로 MNIST 데이터셋을 사용하여 학습을 수행한다. 1. 2층 신경망 클래스 구현하기 import sys,os sys.path.append(os.pardir) from common.functions import * from common.gradient import numer..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. def function_2(x): return x[0]**2 + x[1]**2 기울기 모든 변수의 편미분을 벡터로 정리한 것을 기울기(gradient)라고 한다. def numerical_gradient(f,x): h=1e-4 #0.0001 grad=np.zeros_like(x) for idx in range(x.size): tmp_val=x[idx] #f(x+h) 계산 x[idx]=tmp_val + h fxh1=f(x) #f(x-h) 계산 x[idx]=tmp_val - h fxh2=f(x) grad[idx]=(fxh1-fxh2) / (2*h) x[idx] = tmp_val return grad 그런데 이 기울기라는 게 의미하는 것이 무..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 기계학습 문제는 데이터를 훈련 데이터와 시험 데이터로 나눠 학습과 실험을 수행하는 것이 일반적이다. 그 이유는 우리가 원하는 것은 범용적으로 사용할 수 있는 모델이기 때문이다. 이 범용 능력을 제대로 평가하기 위해 훈련 데이터와 시험 데이터를 분리하는 것이다. 범용 능력은 아직 보지 못한 데이터(훈련 데이터에 포함되지 않은 데이터)로도 문제를 올바르게 풀어내는 능력이다. 그래서 데이터셋 하나로만 매개변수의 학습과 평가를 수행하면 올바른 평가가 될 수 없다. 참고로 한 데이터셋에만 지나치게 최적화된 상태를 오버피팅(overfitting)라고 한다. 손실함수 신경망은 지표를 기준으로 최적의 매개변수 값을 탐색한다. 이를 손실 함수(loss ..

이 포스팅은 밑바닥부터 시작하는 딥러닝 책을 공부하고 정리한것 입니다. 이번 절에서는 이미 학습된 매개변수를 사용하여 학습 과정은 생략하고 추론 과정만 구현한다. 이 추론 과정을 신경망의 순전파(forward propagation)라고도 한다. MNIST의 이미지 데이터는 28x28 크기의 회색조 이미지(1채널)이며, 각 픽셀은 0에서 255까지의 값을 취한다. import sys,os sys.path.append(os.pardir) from dataset.mnist import load_mnist (x_train,t_train),(x_test,t_test) = load_mnist(flatten=True,normalize=False) print(x_train.shape) print(t_train.shap..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 앞에서 배운 퍼셉트론의 장점은 복잡한 함수를 표현할 수 있다는 것이다. 그러나 단점은 가중치를 설정하는 작업은 여전히 사람이 수동으로 한다는 점이다. 신경망이 이러한 단점을 커버해준다. 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습하는 능력이 이제부터 살펴볼 신경망의 중요한 성질이다. 퍼셉트론에서 신경망으로 여기서는 입력,은닉,출력층을 순서대로 0층,1층,2층 이라 하겠다. 그림 3-1의 신경망은 모두 3층으로 구성된다. 가중치를 갖는 층은 2개뿐이기 때문에 2층 신경망이라고 한다. 위 그림에서는 가중치가 b이고 입력이 1인 뉴런이 추가되었다. 이 퍼셉트론의 동작은 x1,x2,1 이라는 3개의 신호가 뉴런에 입력되어, 각 신호..

이 포스팅은 밑바닥부터 시작하는 딥러닝을 공부하고 정리한것 입니다. 퍼셉트론은 프랑크 로젠블라트가 1957년에 고안한 알고리즘으로 신경망(딥러닝)의 기원이 되는 알고리즘이다. 퍼셉트론이란? 퍼셉트론은 다수의 신호를 받아 하나의 신호를 출력한다. x1,x2는 입력 신호, y는 출력 신호, w1과 w2는 가중치를 뜻한다. 그림의 원을 뉴런 혹은 노드라고 부른다. 입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다. 뉴런에서 보내온 신호의 총합이 정해진 한계를 넘어설 때만 1을 출력한다. 그 한계를 입계값이라 하며 기호 세타로 나타낸다. 퍼셉트론 구현하기 def AND(x1,x2): w1,w2,theta= 0.5,0.5,0.7 tmp=x1* w1 + x2 * w2 if tmptheta: return..