GAN을 훈련할 때, 제일 이상적인 상태는 판별기와 생성기가 균형을 이룬 상태이다. 이렇게 되면 판별기는 더는 생성된 데이터와 실제 데이터를 구별하지 못한다. 이 균형이 도달했을 때 판별기의 손실이 어떻게 되는지 확인해보자.
- MSE 손실
평균제곱오차 손실의 정의는 간단하다. 출력 노드에서 나온 값과 원하는 목푯값 사이의 차이를 계산하면 된다. 이 오차를 제곱한다면 값은 항상 양이다. 평균제곱오차는 이 제곱한 오차들의 평균이다.
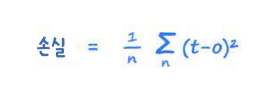
판별기의 결과가 0.5인 이유는 데이터가 생성된 것인지, 진짜인지 양쪽 다 같은 크기로 잘 판단할 수 없다는 의미이다.
출력이 0.5이고 목표가 1이라면 오차는 0.5일 것이다. 반대로 목표가 0이면 오차는 -0.5이다. 두 오차 모두 제곱하면 결과는 0.25가 된다. 따라서 균형 잡힌 GAN의 MSE 손실은 0.25가 된다.
- BCE 손실
이진 교차 엔트로피 손실은 확률과 불확실성에 기반을 둔다.
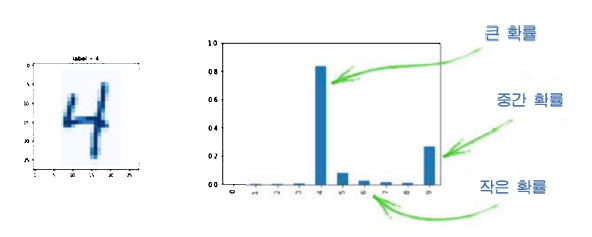
이 그림은 4의 이미지를 분류한 결과이다. 네트워크는 네 번째 노드에 제일 큰 확률을 부여했으며, 이는 이미지가 4일 가느성이 제일 높다는 뜻이다.

2행에서는 분류 결과가 0.1로 확률이 작다. 신경망은 이를 정답이라고 생각하지 않았다는 뜻이다. 목푯값은 1.0이므로 굉장히 많이 틀린 것이다. 좋은 손실함수라면 이 결과에 대해 굉장히 높은 손실값을 부여해야 마땅하다.
이제 확률의 불확실성으로 주제를 넘어가보자.
엔트로피는 불확실성을 설명하는 수학적 아이디어이다. 양면 다 앞인 동전이 있다면 던져서 앞면이 나올 확률은 100%이고, 뒷면이 나올 확률은 0%이다. 두 결과 모두 100% 확률로 예측이 가능하다. 이러한 식으로 불확실성이 0이면 엔트로피 역시 0이라고 할 수 있다.
하지만 일반적인 동전은 던졌을 때 앞면이나 뒷면이나 같은 확률로 나온다. 이러한 경우 불확실성은 최대화 되고, 엔트로피 역시 최대가 된다.

엔트로피는 모든 가능한 결과의 합이며, p는 결과에 대한 확률이다.

앞면만 나오는 동전이라면 p(앞면)=1 이고 불확실성은 0이라는 것을 볼 수 있다.
이제 동전이 앞면만 있을 때, 즉 p(앞면)=1일 때 엔트로피를 계산해보자.

그렇다면 교차 엔트로피(cross entropy)에 대해 알아보자. 이는 실제 결과가 도출될 우도와 우리가 생각하는 우도 사이의 차이에 따른 결과의 불확실성에 대한 지표이다.
동전 예제로 돌아가보면, 우리가 생각하기에 동전이 공정하지만, 실제 결과가 그렇지 않다면 꽤나 놀랄 것이다. 따라서 그 결과에 대해 불확실성이 존재한다고 말할 수 있다. 교차 엔트로피가 말하고자 하는 것이 이 부분이다. 우리가 생각하기에 동정이 공정하고, 실제로도 동일하다면 결과에 대해 그다지 놀랄 일은 없을 것이다. 이때는 교차 엔트로피가 낮은 상태이다.
교차 엔트로피를 두 확률분포의 차이라고 생각할 수 있다. 두 분포의 차이가 없는 만큼 교차 엔트로피도 낮아진다. 정확히 일치한다면 교차 엔트로피는 0이다.
신경망의 출력 결과가 확률분포이고, 실제 결과도 확률분포라고 생각해보자. 이 두 분포가 다르다면 교차 엔트로피는 높고, 둘이 비슷하다면 교차 엔트로피는 낮을 것이다.
수식으로 설명하면 다음과 같이 풀이할 수 있다.

모든 확률에 대한 합을 구했다. x는 분류를 통해 관측된 확률값이고, y는 해당 분류에서의 실제 확률이다.

예측 결과 x가 0.9였는데 정답은 1.0이었어야 한다. 여기서 모든 가능한 분류 확률을 더하면 나올 수 있는 값은 1.0과 그 반대인 0.0이다.

또한 정답이 1.0이었는데 예측 결과가 0.1이었을 때의 예제에 대해서도 교차 엔트로피를 계산해보자.


처음 두 행을 통해 잘못 맞힌 경우 교차 엔트로피가 커진다는 것을 알 수 있고, 정답에 가깝게 맞히면 이 값이 작다는 것을 알 수 있다. 세 번째 행을 통해, 확실하게 틀린 값에 대해서도 교차 엔트로피가 크다는 점을 알 수 있다. 이를 통해 교차 엔트로피를 손실함수로 쓰는 것이 유용하다는 사실을 알 수 있다.
교차 엔트로피를 사용하는 핵심적인 이유는 잘못된 답에 대해 훨씬 큰 피드백을 주기 때문이다.

이진 교차 엔트로피는 이진 분류 문제에서 쓰는 교차 엔트로피이다. 판별기 중에 참을 1.0, 거짓을 0.0으로 표시하는 신경망이 대표적으로 이 손실함수를 쓴다고 할 수 있다.
다시 돌아가서 판별기와 생성기가 균형이 맞을 때 이진 교차 엔트로피 손실값은 어떤 값이어야 할까? 판별기는 진짜와 가짜를 구별해내는 데 무차별해야 하므로 결과는 항상 0.5여야 한다. 어떤 값들이 1.0이라면 나머지 다른 값들은 0.0이어야 한다.
x=0.5, y=1.0 일때 교차 엔트로피는 다음과 같이 구한다.
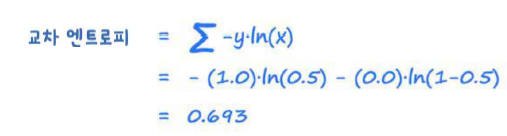
x=0.5, y=0.0 일 때 교차 엔트로피의 계산 결과는 다음과 같다.
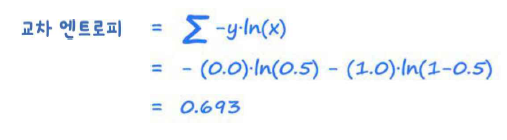
따라서 BCELoss()를 쓸 때 GAN의 이상적인 손실값은 0.693이 된다.
'GAN > 이론' 카테고리의 다른 글
| 8. 조건부 GAN (0) | 2021.11.08 |
|---|---|
| 7. 합성곱 GAN (전치 합성곱) (0) | 2021.11.06 |
| 6. 얼굴 이미지(HDF5 데이터 형식, GPU 가속) (0) | 2021.11.06 |
| 5. 손으로 쓴 숫자 훈련(2) (0) | 2021.11.03 |
| 4. 손으로 쓴 숫자 훈련 (1) (0) | 2021.11.03 |