현재의 DeZero는 미분을 자동으로 계산할 수 있지만 1차 미분 한정이다. 그래서 이번 단계에서는 2차 미분도 자동으로 계산할 수 있도록, 나아가 3차 미분, 4차 미분... 형태의 모든 고차 미분까지 자동으로 계산할 수 있도록 DeZero를 확장할 것이다.
- 역전파 계산
순전파와 마찬가지로 역전파에도 구체적인 계산 로직이 있다. 하지만 현재의 DeZero는 계산과 관련한 아무런 계산 그래프도 만들지 않는다. 왜냐하면 이 계산에서는 ndarray 인스턴스가 사용되기 때문이다. 만약 역전파를 계산할 때도 '연결'이 만들어진다면 고차 미분을 자동으로 계산할 수 있게 된다.


위 그림은 sin함수의 미분을 구하기 위한 계산 그래프이다. 만약 위와 같은 계산 그래프가 있다면 gx.backward()를 호출하여 gx의 x에 대한 미분을 계산할 수 있다. 원래 gx는 y=sin(x)의 미분이기 때문에 gx.backward()를 호출함으로써 x에 대한 미분이 한 번 더 이루어진다. 즉 이것이 2차 미분에 해당한다.
- 역전파로 계산 그래프 만들기
함수의 backward 메서드에서 ndarray 인스턴스가 아닌 Variable 인스턴스를 사용하면 계산의 '연결'을 만들 수 있다.
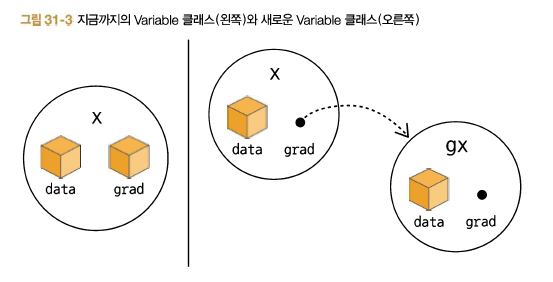
이렇게 변경하면 y=sin(x)를 다음 그림과 같은 계산 그래프로 표현할 수 있다.

위 그림은 y.backward()를 호출함으로써 '새로' 만들어지는 계산 그래프이다. 위와 같은 계산 그래프가 있다면 gx.backward()를 호출함으로써 y의 x에 대한 2차 미분이 이루어진다.
- Variable 클래스 수정
def backward(self,retain_grad=False,create_graph=False): if self.grad is None: self.grad = Variable(np.ones_like(self.data))
self.grad가 Variable 인스턴스를 담게 된다.
- 함수들의 backward 메서드 수정

수정 후에는 Mul 클래스에서 Variable 인스턴스를 그대로 사용한다. 여기서 중요한 점은 역전파를 계산하는 gy * x1 코드이다. gy와 x1은 Variable 인스턴스이기 때문에 gy * x1 이 실행되는 뒤편에선는 Mul 클래스의 순전파가 호출된다. 그때 Function.__call__이 호출되고, 그 안에서 계산 그래프가 만들어진다.
- 2차 미분 계산하기
y=x^4 - 2x^2 이라는 수식의 2차 미분을 계산해보자.
def f(x):
y=x**4 - 2 * x ** 2
return y
x=Variable(np.array(2.0))
y=f(x)
y.backward(create_graph=True)
print(x.grad)
gx=x.grad
x.cleargrad()
gx.backward()
print(x.grad)
'Deep learning > 모델 구현' 카테고리의 다른 글
| 34. 신경망 (0) | 2021.10.17 |
|---|---|
| 33. 형상 변환 함수, 합계 함수 (0) | 2021.10.16 |
| 31. 함수 최적화(중요) (0) | 2021.10.12 |
| 30. 테일러 급수 미분 (0) | 2021.10.12 |
| 29. 연산자 오버로드 (0) | 2021.10.10 |