- sin 함수 구현
Sin 클래스와 sin 함수는 다음처럼 구현할 수 있다.
class Sin(Function):
def forward(self,x):
y=np.sin(x)
return y
def backward(self,gy):
x=self.inputs[0].data
gx=gy * np.cos(x)
return gx
def sin(x):
return Sin()(x)
- 테일러 급수 이론
Sin 함수의 미분은 다음과 같은 테일러 급수를 이용한 방법으로 계산할 수 있다. 테일러 급수란 어떤 함수를 다항식으로 근사하는 방법으로, 수식으로는 다음과 같다.
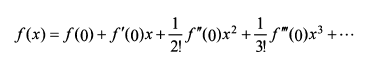
여기서 f(x)=sin(x)를 위 식에 적용시켜 보면 다음과 같은 식이 나온다.

위 식에서 보듯 sin 함수는 x의 거듭제곱으로 이루어진 항들이 무한히 계속되는 형태로 표현된다. 여기서 중요한 점은 시그마의 i가 커질수록 근사 정밀도가 좋아진다는 것이다. 또한 i가 커질수록 시그마 뒤의 항의 절대값은 작아지므로, 이 값을 참고하여 i의 값(반복 횟수)을 적절히 결정할 수 있다.
import math
def my_sin(x,threshold=0.0001):
y=0
for i in range(100000):
c=(-1) ** i / math.factorial(2*i+1)
t=c*x**(2*i+1)
y=y+t
if abs(t.data) < threshold:
break
return y
'Deep learning > 모델 구현' 카테고리의 다른 글
| 32. 고차 미분 (0) | 2021.10.14 |
|---|---|
| 31. 함수 최적화(중요) (0) | 2021.10.12 |
| 29. 연산자 오버로드 (0) | 2021.10.10 |
| 28. 변수 사용성 개선 (0) | 2021.10.10 |
| 27. 메모리 관리 (0) | 2021.10.04 |