이 포스팅은 혼자 공부하는 머신러닝 + 딥러닝 책을 공부하고 정리한것 입니다.
비지도 학습
타깃을 모르는 사진을 종류별로 분류하려 할때 사용하는 머신러닝 알고리즘이 바로 비지도 학습이다(unsupervised learning) 사람이 가르쳐 주지 않아도 데이터에 있는 무언가를 학습하게 된다.
과일 데이터는 사과, 바나나, 파인애플을 담고 이는 흑백 사진이다. 이 데이터는 넘파이 배열의 기본 저장 포맷인 npy파일로 저장되어 있다. 넘파이에서 이 파일을 읽으려면 먼저 코랩으로 다운로드 해야한다.
!wget https://bit.ly/fruits_300_data -O fruits_300.npy

import numpy as np
import matplotlib.pyplot as plt
fruits=np.load('fruits_300.npy')
print(fruits.shape)

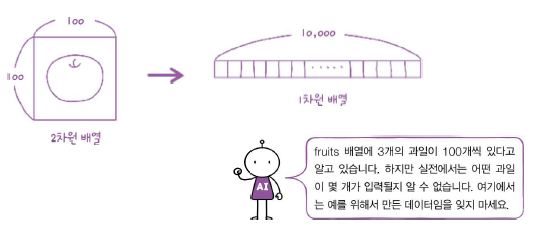
이 배열의 첫번째 차원(300)은 샘플의 개수를 나타내고, 두 번째 차원(100)은 이미지 높이, 세 번째 차원(100)은 이미지 너비이다. 이미지 크기는 100x100이다. 각 픽셀은 넘파이 배열의 원소 하나에 대응한다. 즉 배열의 크기가 100x100이다.
첫 번째 이미지의 첫번째 행을 출력하겠다.
print(fruits[0,0,:])

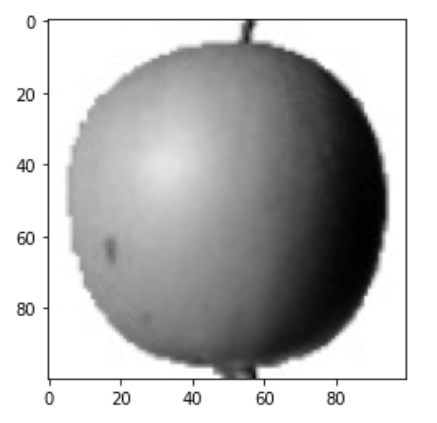
plt.imshow(fruits[0],cmap='gray') plt.show()

보통 흑백 샘플 이미지는 바탕이 밝고 물체가 짙은 색이다. 그 이유는 이 흑백 이미지는 사진으로 찍은 이미지를 넘파이 배열로 변환할 대 반전시켰기 때문이다.
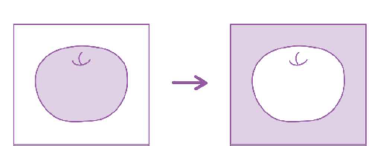
이렇게 바꾼 이유는 우리의 관심 대상은 바탕이 아니라 사과이기 때문이다. 흰색 바탕은 우리에게 중요하지 않지만 컴퓨터는 255에 가까운 바탕에 집중할 것이다. 따라서 바탕을 검게 만들고 사진에 짙게 나온 사과를 밝은색으로 만들었다.
plt.imshow(fruits[0],cmap='gray_r') plt.show()
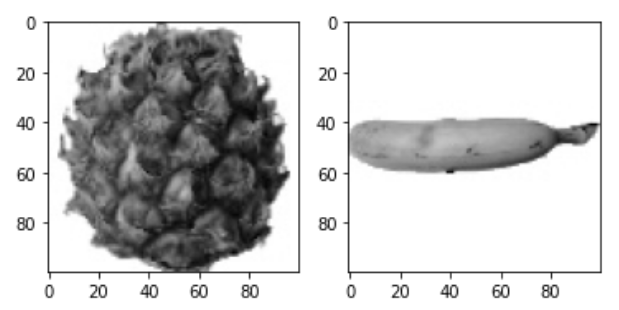
맷플롯립의 subplots() 함수를 사용하면 여러 개의 그래프를 배열처럼 쌓을 수 있도록 도와준다. subplots() 함수의 두 매개변수는 그래프를 쌓을 행과 열을 지정한다.
반환된 axs는 2개의 서브 그래프를 담고 있는 배열이다. axs[0]에 파인애플 이미지를, 그리고 axs[1]에 바나나 이미지를 그렸다. 이 장에서 subplots()를 사용해 한 번에 여러 개의 이미지를 그려보자.
fig,axs=plt.subplots(1,2) axs[0].imshow(fruits[100],cmap='gray_r') axs[1].imshow(fruits[200],cmap='gray_r') plt.show()
픽셀값 분석하기
사용하기 쉽게 fruits 데이터를 사과, 파인애플, 바나나로 각각 나누어 보자. 넘파이 배열을 나눌때 100x100 이미지를 펼쳐서 길이가 10000인 1차원 배열로 만들겠다. 이렇게 펼치면 이미지로 출력하긴 어렵지만 배열을 계산할 때 편리하다.
apple=fruits[0:100].reshape(-1,100*100) pineapple=fruits[100:200].reshape(-1,100*100) banana=fruits[200:300].reshape(-1,100*100) print(apple.shape)
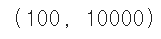
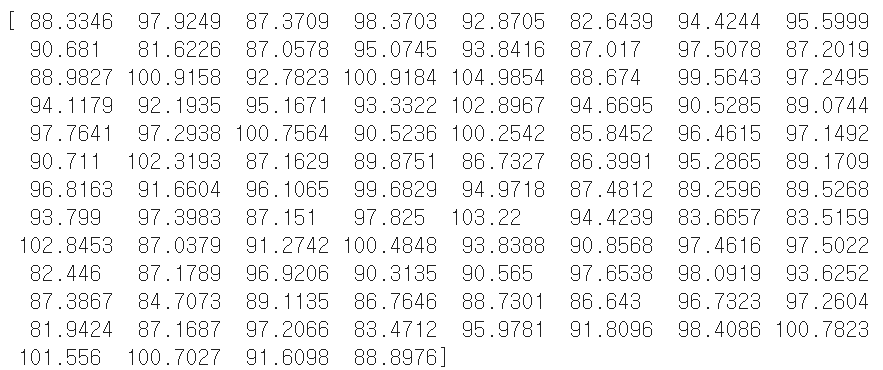
print(apple.mean(axis=1))
히스토그램을 그려보면 평균값이 어떻게 분포되어 있는지 한눈에 잘 볼 수 있다.

plt.hist(np.mean(apple,axis=1),alpha=0.8) plt.hist(np.mean(pineapple,axis=1),alpha=0.8) plt.hist(np.mean(banana,axis=1),alpha=0.8) plt.legend(['apple','pineapple','banana']) plt.show()
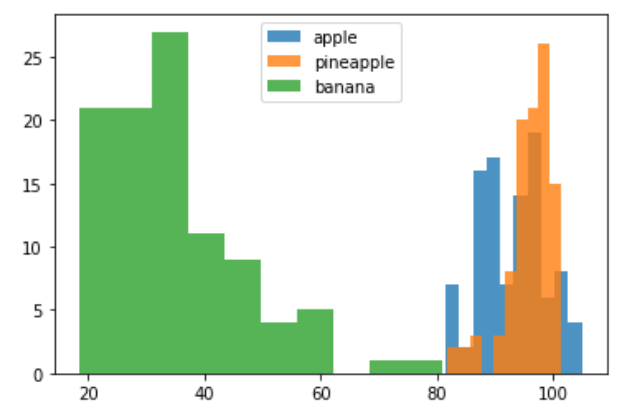
alpha 매개변수를 1보다 작게 하면 투명도를 줄 수 있다.
샘플의 평균값만으로 바나나는 사과나 파인애플과 확실히 구분된다. 바나나는 사진에서 차지하는 영역이 작기 때문에 평균값이 작다. 반면 사과와 파인애플은 많이 겹쳐져있어서 픽셀값만으로는 구분하기 쉽지 않다. 사과나 파인애플은 대체로 형태가 둥그랗고 사진에서 차지하는 크기도 비슷하기 때문이다.
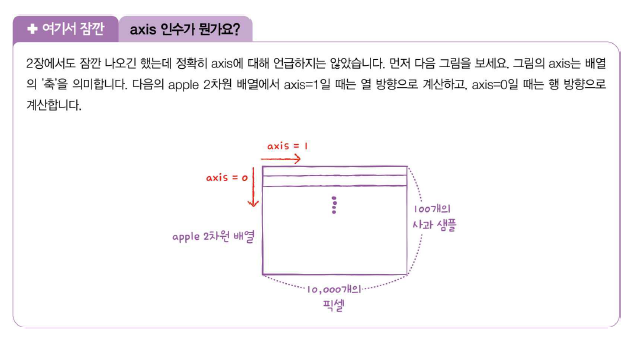
픽셀별 평균값을 비교해보는 방법을 이용해 보자. 세 과일은 모양이 다르므로 픽셀값이 높은 위치가 조금 다를 것 같다. 픽셀의 평균을 계산하는 것은 간단하다. axis=0으로 지정하면 된다.
fig,axs=plt.subplots(1,3,figsize=(20,5)) axs[0].bar(range(10000),np.mean(apple,axis=0)) axs[1].bar(range(10000),np.mean(pineapple,axis=0)) axs[2].bar(range(10000),np.mean(banana,axis=0)) plt.show()
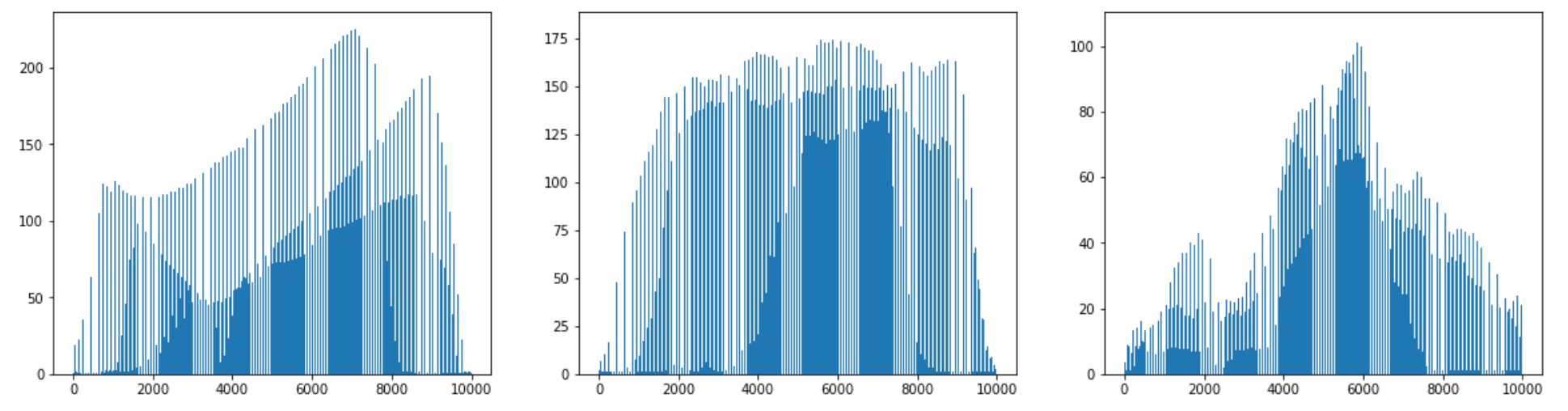
픽셀 평균값을 100 x 100 크기로 바꿔서 이미지처럼 출력하여 위 그래프와 비교하면 더 좋다. 픽셀을 평균 낸 이미지를 모든 사진을 합쳐놓은 대표 이미지로 생각할 수 있다.
apple_mean=np.mean(apple,axis=0).reshape(100,100) pineapple_mean=np.mean(pineapple,axis=0).reshape(100,100) banana_mean=np.mean(banana,axis=0).reshape(100,100) fig,axs=plt.subplots(1,3,figsize=(20,5)) axs[0].imshow(apple_mean,cmap='gray_r') axs[1].imshow(pineapple_mean,cmap='gray_r') axs[2].imshow(banana_mean,cmap='gray_r') plt.show()
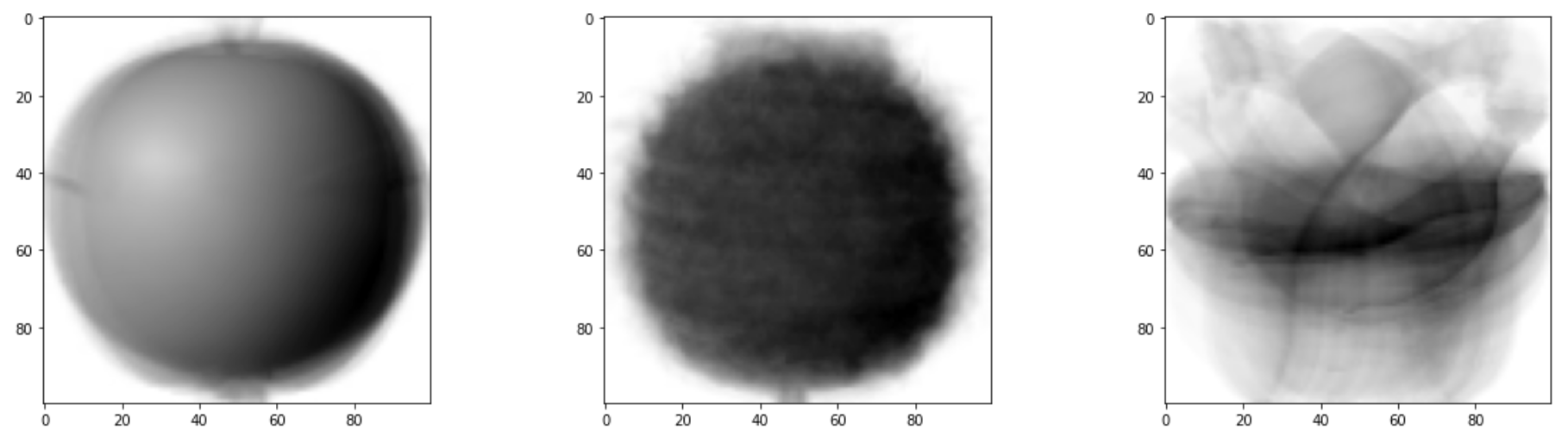
세 과일은 픽셀 위치에 따라 값의 크기가 차이 난다. 따라서 이 대표 이미지와 가까운 사진을 골라 낸다면 사과, 파인애플, 바나나를 구분할 수 있을것 같다.
평균값과 가까운 사진 고르기
사과 사진의 평균값인 apple_mean과 가장 가까운 사진을 골라보자. 앞에서 봤던 절댓값 오차를 사용하겠다. fruits 배열에 있는 모든 샘플에서 apple_mean을 뺸 절대값의 평균을 계산하면 된다.
다음 코드에서 abs_diff는 (300,100,100) 크기의 배열이다. 따라서 각 샘플에 대한 평균을 구하기 위해 axis에 두번째, 세번째 차원을 모두 지정했다. 이렇게 계산한 abs_mean은 각 샘플의 오차 평균이므로 크기가 (300,)인 1차원 배열이다.
abs_diff=np.abs(fruits-apple_mean) abs_mean=np.mean(abs_diff,axis=(1,2)) print(abs_mean.shape)
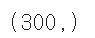
그다음, 이 값이 가장 작은 순서대로 100개를 골라보자. 즉 apple_mean과 오차가 가장 작은 샘플 100개를 고르는 것이다. np.argsort() 함수는 작은 것에서 큰 순서대로 나열한 abs_mean 배열의 인덱스를 반환한다. 이 인덱스 중에서 처음 100개를 선택해 10x10 격자로 이루어진 그래프를 그리겠다.
apple_index=np.argsort(abs_mean)[:100]
fig,axs=plt.subplots(10,10,figsize=(10,10))
for i in range(10):
for j in range(10):
axs[i,j].imshow(fruits[apple_index[i*10+j]],cmap='gray_r')
axs[i,j].axis('off')
plt.show()

결론
흑백 사진에 있는 픽셀값을 사용해 과일 사진을 모으는 작업을 해 보았다. 이렇게 비슷한 샘플끼리 그룹으로 모으는 작업을 군집(clustering) 이라고 한다. 군집은 대표적인 비지도 학습 작업 중 하나이다. 군집 알고리즘에서 만든 그룹을 클러스터(cluster) 라고 부른다.
우리는 이미 타깃값을 알고 있었기 때문에 사과, 파인애플, 바나나의 사진 평균값을 계산해서 가장 가까운 과일을 찾을 수 있었다. 실제 비지도 학습에서는 타깃값을 모르기 때문에 이처럼 샘플의 평균값을 미리 구할 수 없다.
다음에 배울 k-평균 알고리즘이 타깃값을 모르면서도 세 과일의 평균값을 찾을 수 있다.
'Machine Learning > Basic' 카테고리의 다른 글
| [6-3] 주성분 분석 (0) | 2021.04.13 |
|---|---|
| [6-2] k-평균 (0) | 2021.04.13 |
| [5-3-(2)] 트리의 앙상블 - 엑스트라 트리, 그레이디언트 부스팅, 히스토그램 기반 그레이디언트 부스팅 (0) | 2021.04.10 |
| [5-3-(1)] 트리의 앙상블 - 랜덤 포레스트 (0) | 2021.04.10 |
| [5-2] 교차 검증과 그리드 서치 (0) | 2021.04.07 |