https://leetcode.com/problems/fibonacci-number/
Fibonacci Number - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
1. 재귀 구조 브루트 포스
class Solution:
def fib(self, n: int) -> int:
if N<=1:
return N
return self.fib(N-1) + self.fib(N-2)이 방식은 가능한 풀이 방법 중에서 가장 느릴 것이다.
2. 메모이제이션
이전 포스팅에서 다이나믹 프로그래밍의 하향식 풀이로 정리한 것이 바로 이 문제의 메모이제이션 풀이다.
class Solution:
dp=collections.defaultdict(int)
def fib(self, n: int) -> int:
if n<=1:
return n
if self.dp[n]:
return self.dp[n]
self.dp[n] = self.fib(n-1) + self.fib(n-2)
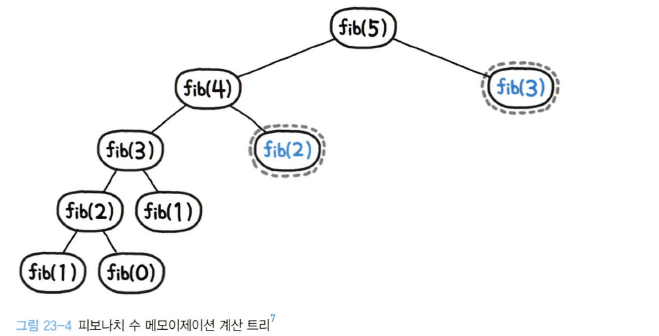
return self.dp[n]이미 계산한 값은 저장해뒀다가 바로 리턴한다. 앞서 fib(5)일 때 15번의 연산을 진행하던 구조는 이 메모이제이션 풀이에서는 아래 그림과 같이 9번의 연산만으로 풀이할 수 있게 된다.

3. 타뷸레이션
class Solution:
dp=collections.defaultdict(int)
def fib(self, n: int) -> int:
self.dp[1]=1
for i in range(2,n+1):
self.dp[i] = self.dp[i-1] + self.dp[i-2]
return self.dp[n]재귀를 사용하지 않고 반복으로 풀이하며, 작은 값부터 직접 계산하면서 타뷸레이션한다. 미리 계산을 해두는 것인데, 다른 복잡한 다이나믹 프로그래밍 문제와는 달리 타뷸레이션이 일차원 선형 구조라 복잡하지 않고 구조 자체도 단순해 이해가 쉬운 편이다. 메모이제이션과 마찬가지로 실행 속도도 당연히 빠르다.
4. 두 변수만 이용해 공간 절약
앞선 풀이들은 dp라는 딕셔너리에 결과를 담아 나갔지만 변수는 2개만 있어도 충분하다.
class Solution:
#dp=collections.defaultdict(int)
def fib(self, n: int) -> int:
x,y=0,1
for i in range(0,n):
x,y=y,x+y
return x이 경우 앞서 풀이처럼 메소드 바깥에 클래스의 멤버 변수도 선언할 필요가 없어 더 간결하다. 공간 복잡도도 O(n)에서 O(1)로 줄어든다. 시간 복잡도는 동일한 O(n)이므로 효율적이다.
'알고리즘 > DP' 카테고리의 다른 글
| 백준 - 쉬운계단수(10844번) (DP) (0) | 2022.08.03 |
|---|---|
| 백준 - 포도주 시식(2156번) - 배열 내에서 조건에 맞는 최대값 찾기(DP) (0) | 2022.08.03 |
| 다이나믹 프로그래밍 (0) | 2022.05.21 |