힙은 힙의 특성(최소 힙에서는 부모가 항상 자식보다 작거나 같다)을 만족하는 거의 완전한 이진 트리인 특수한 트리 기반의 자료구조다.
파이썬에서는 최소 힙만 구현되어 있고 heapq모듈로 사용할 수 있다. 최소 힙은 부모가 항상 자식보다 작기 때문에 루트가 결국 가장 작은 값을 갖게 되며, 우선순위 큐에서 가장 작은 값을 추출하는 것은 매번 힙의 루트를 가져오는 형태로 구현된다.
우선순위 큐는 주로 힙으로 구현하고, 힙은 주로 배열로 구현한다. 따라서 우선순위 큐는 결국은 배열로 구현하는 셈이 된다.
힙은 정렬된 구조가 아니다. 최소 힙의 경우 부모 노드가 항상 작다는 조건만 만족할 뿐, 서로 정렬되어 있지 않다.


계산을 편하게 하기 위해 인덱스는 1부터 사용한다.
힙 연산
먼저 이진 힙을 구현하기 위한 클래스 정의부터 진행해보자.
class BinaryHeap(object):
def __init__(self):
self.items=[None]
def __len__(self):
return len(self.items) - 1
__len__() 처럼 밑줄 2개로 둘러싸인 함수는 파이썬의 매직 메소드로 여러 가지 내부 기능이 동작되는 데 사용된다.
0번 인덱스는 사용하지 않기 위해 None을 미리 설정해뒀다.
1. 삽입
힙에 요소를 삽입하기 위해서는 업힙 연산을 수행해야 한다. 일반적으로 업힙 연산은 percolate_up() 이라는 함수로 정의한다. 힙에 요소를 삽입하는 과정은 다음과 같다.
1. 요소를 가장 하위 레벨의 최대한 왼쪽으로 삽입한다.(배열로 표현할 경우 가장 마지막에 삽입한다).
2. 부모 값과 비교해 값이 더 작은 경우 위치를 변경한다.
3. 계속해서 부모 값과 비교해 위치를 변경한다(가장 작은 값일 경우 루트까지 올라감).

def _percolate_up(self):
i=len(self)
parent=i//2
while parent>0:
if self.items[i] < self.items[parent]:
self.items[parent],self.items[i] = self.items[i],self.items[parent]
i=parent
parent=i//2
def insert(self,k):
self.items.append(k)
self._percolate_up()
2. 추출
루트를 추출하면 된다. 추출 이후에 다시 힙의 특성을 유지하는 작업이 필요하기 때문에 시간복잡도는 O(log n)이다.
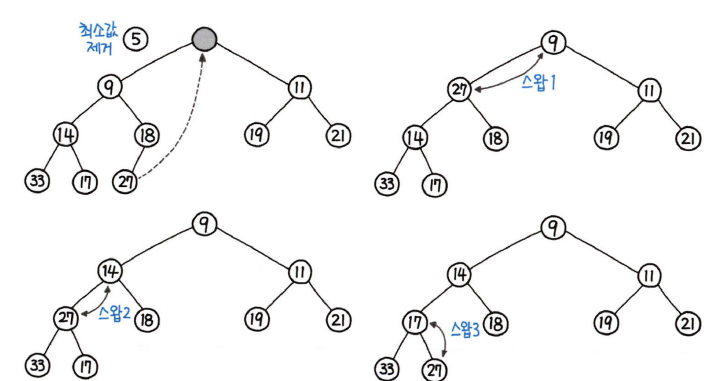
def _percolate_down(self,idx):
left=idx*2
right=idx*2 + 1
smallest=idx
if left<=len(self) and self.items[left] < self.items[smallest]:
smallest=left
if right<=len(self) and self.items[right] < self.items[smallest]:
smallest=right
if smallest != idx:
self.items[idx] , self.items[smallest]=self.items[smallest],self.items[idx]
self._percolate_down(smallest)
def extract(self):
extracted=self.items[1]
self.items[1] = self.items[len(self)]
self.items.pop()
self._percolate_down(1)
return extracted
기존 파이썬 heap 모듈의 heapq.heappush()는 insert()에, heapq.heappop()은 extract()에 대응된다.

'알고리즘' 카테고리의 다른 글
| 이진 검색 (0) | 2022.05.16 |
|---|---|
| 힙을 사용한 예제(배열의 k번째 큰 요소) (0) | 2022.05.11 |
| 전위, 중위 순회 결과를 이용해 이진 트리 구축 (0) | 2022.05.10 |
| 파이썬 sort함수 key 기술 (0) | 2022.05.10 |
| 문자열을 숫자 리스트로 각 자리마다 분해하기 (0) | 2022.05.02 |