지금까지 Variable 클래스와 Function 클래스를 구현했다. 이 클래스들을 구현한 이유는 미분을 자동으로 계산하기 위해서이다.
수치 미분을 구현하기 전에 수치 미분에 대해 알아보겠다.
수치 미분은 작은 값을 사용하여 진정한 미분을 근사한다. 따라서 값에 어쩔 수 없이 오차가 포함되는데, 이 근사 오차를 줄이는 방법으로는 중앙차분이라는게 있다.

def numerical_diff(f,x,eps=1e-4):
x0=Variable(x.data - eps)
x1=Variable(x.data + eps)
y0=f(x0)
y1=f(x1)
return (y1.data - y0.data) / (2 * eps)
다음 코드 처럼 합성 함수의 미분을 구현할 수 있다.
def f(x):
A=Square()
B=Exp()
C=Square()
return C(B(A(x)))
x=Variable(np.array(0.5))
dy=numerical_diff(f,x) # 파이썬에서는 함수도 객체이기 때문에 다른 함수에 인수로 전달 할 수 있다
print(dy)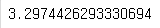
수치 미분의 문제점
수치 미분의 결과에는 오차가 포함되어 있다. 대부분의 경우 오차는 매우 작지만 어떤 계산이냐에 따라 커질 수도 있다.

수치 미분의 더 심각한 문제는 계산량이 많다는 점이다.
수치 미분은 구현하기 쉽고 거의 정확한 값을 얻을 수 있다. 이에 비해 역전파는 복잡한 알고리즘이라서 구현하면서 버그가 섞여 들어가기 쉽다. 그래서 역전파를 정확하게 구현했는지 확인하기 위해 수치 미분의 결과를 이용하곤 한다. 이를 기울기 확인 이라고 하는데, 단순히 수치 미분 결과와 역전파의 결과를 비교하는 것이다.
'Deep learning > 모델 구현' 카테고리의 다른 글
| 23. 역전파 자동화 (0) | 2021.09.29 |
|---|---|
| 22. 역전파 (0) | 2021.09.29 |
| 20. 변수와 함수 (0) | 2021.09.28 |
| 19. CNN(6) - CNN 시각화하기, 대표적인 CNN (0) | 2021.04.26 |
| 18. CNN(5) - CNN 구현하기 (0) | 2021.04.25 |